Densité d'énergie - Définition

Relativité générale

En relativité générale, les équations déterminant le champ gravitationnel se déduisent par un analogue de l'équation de Poisson en gravitation universelle, à savoir :

,

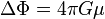
où Δ représente l'opérateur laplacien, Φ le potentiel gravitationnel, G la constante de gravitation et μ la densité de masse (ou masse volumique). En relativité générale, cette équation est remplacée par un jeu d'équations plus complexes : les équations d'Einstein. Dans ce contexte, une version simplifiée de ces équations révèle que le potentiel gravitationnel Φ est remplacé par la quantité sans dimension Φ/c² et la masse volumique par la densité d'énergie. Ainsi, la nouvelle équation de Poisson est-elle de la forme :

,

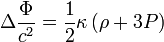
où la quantité κ est appelée constante d'Einstein et vaut :

,

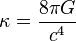
ρ et P correspondant respectivement à la densité d'énergie et à la pression. Ceci indique que c'est l'énergie et non la masse qui produit le champ gravitationnel, conformément à la célèbre relation E=mc² découverte par Albert Einstein en 1905. Parmi les conséquences de cette relation, un corps chaud (contenant des photons et donc une densité d'énergie électromagnétique non nulle) génère un champ gravitationnel plus important qu'un corps identique de température moindre.

Ceci signifie que l'on peut, dans une interprétation newtonienne, associer une certaine masse à une région dont la densité d'énergie est non nulle, même si cette densité d'énergie provient d'objets de masse nulle. Ainsi, un gaz de photon à température ambiante (environ 300 kelvins) « pèse »-t-il dans les 6,81′10^-23 kg·m^-3, ce qui reste une densité totalement négligeable par rapport à celle de l'air. Dans des cas extrêmes, la densité d'énergie d'un champ électromagnétique peut être néanmoins considérable. Ainsi, à la surface d'une étoile à neutrons à très fort champ magnétique (un pulsar X anormal), qui peut atteindre 10⁸ teslas, la densité d'énergie associée atteint-elle des valeurs de l'ordre de plusieurs dizaines de tonnes par mètre cube. Ces densité restent cependant faible, dans le contexte d'une étoile à neutrons, donc la densité centrale est supposée être de l'ordre de 10¹⁴ tonnes par mètre cube.