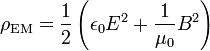Densité d'énergie - Définition

Introduction

En physique, la densité d'énergie représente l'énergie par unité de volume en un point, concernant une forme d'énergie non localisée. Le concept de densité d'énergie est abondamment utilisé en relativité générale et en cosmologie car il intervient explicitement dans les équations déterminant le champ gravitationnel (les équations d'Einstein), mais il est également présent en mécanique des milieux continus et en électromagnétisme.

Mécanique des milieux continus

En termes d'analyse dimensionnelle, la pression correspond à une densité d'énergie. Ce fait possède, en théorie cinétique des gaz, une interprétation simple : la pression est une mesure de l'énergie cinétique microscopique (c'est-à-dire due à l'agitation thermique) des particules composant le gaz. En notant T la température, m la masse des molécules, n la densité de particules et v la norme de la vitesse de chaque particule, on montre en effet que la pression p est liée à l'énergie cinétique moyenne par :

.

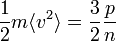
Cette expression se réécrit de façon plus explicite selon

,

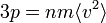
ou bien

,

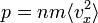
c'est-à-dire que la pression est donnée par le flux de quantité de mouvement selon une direction donnée (noté x ici), c'est-à-dire le produit nmv_x par la vitesse v_x. De fait, un tel flux de quantité de mouvement est égal à un facteur près à la densité d'énergie cinétique, et donc une densité d'énergie.

Champ scalaire

En physique théorique, on peut associer à un objet appelé champ scalaire une densité d'énergie. La densité d'énergie associée à un champ φ s'écrit

,

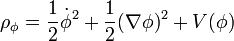
où le point désigne une dérivée par rapport au temps. La densité d'énergie présente donc un terme cinétique (), un terme d'interaction ( ) et un terme potentiel (V(φ)). La formule ci-dessus est donnée en unité dites « relativistes », où la constante de Planck réduite et la vitesse de la lumière valent 1 et où toutes les grandeurs physiques sont ramenées à des puissances d'une énergie. Dans un système d'unité tel le système international d'unités, en supposant que l'on est dans un espace-temps à quatre dimensions et qu'un champ scalaire a la dimension d'une énergie, alors la densité d'énergie devient, en tenant compte de toutes le constantes fondamentales,

,

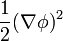
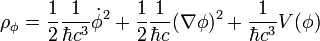
où il a été supposé (de façon quelque peu arbitraire) que la normalisation du terme de potentiel suivait celle de la mécanique du point, où la relation entre accélération et potentiel était de la forme , ce qui équivaut ici à considérer que dimensionnellement, le potentiel est homogène au carré d'une énergie divisé par un temps.

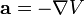
Électromagnétisme

En électromagnétisme, on peut définir la densité d'énergie électrostatique et la densité d'énergie magnétostatique par les formules, données ici dans le vide :

,

,

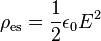
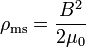
où E et B représentent respectivement le module du champ électrique et du champ magnétique, et ε et μ la permittivité et la perméabilité du vide. En référence à la mécanique des milieux continus, ces densités d'énergie sont parfois appelées « pression électrostatique » et « pression magnétostatique ». Ces formules peuvent être combinées sous la forme

En présence d'ondes électromagnétiques, ces formules peuvent être utilisées pour calculer la densité d'énergie associée à ces ondes. Ceci peut alors de fait donner la densité d'énergie d'un gaz de photons. En particulier, la densité d'énergie associée à un corps noir de température T donnée peut se calculer, et est égale à :

,

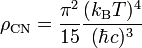
où k, et c représentent respectivement la constante de Boltzmann, la constante de Planck réduite et la vitesse de la lumière.

Dans ce contexte, la pression de radiation s'interprète de façon microscopique comme la poussée exercée par un gaz de photons sur un objet du fait du transfert d'impulsion entre celui-ci et ces derniers.