Densité d'énergie - Définition

Cosmologie

Le concept de densité d'énergie est crucial en cosmologie, car il existe une relation entre une quantité décrivant la géométrie de l'espace (la courbure spatiale), la densité d'énergie totale, et la taux d'expansion de l'univers.

La densité d'énergie d'une espèce évolue au cours du temps différemment selon ses caractéristiques. L'évolution temporelle de la densité d'énergie est décrite par une équation improprement appelée équation de conservation. Dans un univers homogène et isotrope, elle s'écrit

,

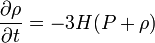
P étant la pression de l'espèce considérée et H le taux d'expansion de l'univers.

Souvent on note par w le rapport de la pression à la densité d'énergie, ce qui permet de réécrire l'équation de conservation ci-dessus comme

.

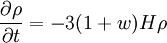
Cette dernière équation permet alors de déterminer comment évolue la densité d'énergie en fonction de l'indication de distance entre deux objets lointains, le facteur d'échelle (que l'on notera a par la suite). On obtient immédiatement

.

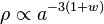
La densité d'énergie varie donc en fonction de la pression de l'espèce considérée. Pour de la matière non relativiste, pour laquelle la pression est négligeable devant la densité d'énergie (correspondant presque entièrement à la densité d'énergie de masse), on a

.

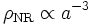
Ce résulte ne fait rien d'autre qu'indiquer que la densité de particules décroît du fait de la dilution due à l'expansion. Pour une espèce relativiste, pour laquelle la quantité w tend vers 1/3, on a

.

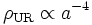
Ici, à l'effet de dilution évoqué ci-dessus, se superpose le fait que les particules considérées voient leur énergie décroître inversement proportionnellement à l'allongement des distances. C'est en réalité le phénomène de décalage vers le rouge bien connu en cosmologie.

Il est important de connaître toutes les contributions possibles à la densité d'énergie totale de l'univers. Ainsi, dans le modèle standard de la cosmologie est-on amené à évaluer les contributions des différentes formes d'énergie existant dans l'univers. l'on sait qu'il existe au moins quatre formes d'énergie distinctes, à savoir les photons, dont le gros de l'énergie est sous la forme du fond diffus cosmologique, les neutrinos, dont le gros de l'énergie est issue du fond cosmologique de neutrinos, la matière baryonique, c'est-à-dire la matière composants les noyaux atomiques (protons, neutrons), et la matière noire. À cela s'ajoute l'énergie noire, dont l'existence est le plus directement mise en évidence par le phénomène d'accélération de l'expansion de l'univers. La donnée des valeurs absolues des densité d'énergie n'est pas très intéressante en cosmologie. Ce qui importe le plus est leur valeur en unités que l'on peut qualifier de « naturelles », c'est-à-dire par rapport à une quantité homogène à une densité d'énergie que l'on appelle densité critique. Dans l'hypothèse où la géométrie de l'univers est « plate » (c'est-à-dire que la courbure spatiale à grande échelle est nulle), alors la densité d'énergie totale doit être égale à la densité critique. Il est donc relativement naturel d'exprimer les différentes densités d'énergie en termes de la densité critique. On définit ainsi le paramètre de densité d'une forme d'énergie par le rapport de sa densité d'énergie à la densité critique.

La densité critique

La relation qui existe entre le taux d'expansion actuel de l'univers et la densité d'énergie totale actuelle de l'univers s'écrit, si la courbure spatiale est nulle,

,

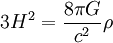
où H représente le taux d'expansion actuel de l'univers, c'est-à-dire la constante de Hubble. La densité critique ρ est alors définie selon

.

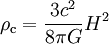
Quand on évalue numérique cette quantité, on est confronté au fait que la valeur exacte de la constante de Hubble n'est pas connue avec précision. Aussi introduit-on souvent la « constante de Hubble réduite », notée h, définie par

,

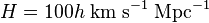
où h est un nombre sans dimension de l'ordre de 0,7. Muni de cette notant, on obtient

.

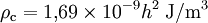
Le fond diffus cosmologique

Le fond diffus cosmologique se présente comme un corps noir quasi parfait, dont la température a été mesurée très précisément par l'instrument FIRAS du satellite artificiel COBE au début des années 1990 à 2,728 K. La densité d'énergie associée est donc, d'après la formule donnée plus haut,

.

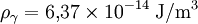
En termes du paramètre de densité, on obtient

.

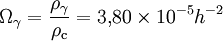
La valeur exacte du paramètre de densité associé n'est pas connue du fait de l'incertitude sur h, mais le paramètre est en tout état de cause très petit. D'ordinaire on écrit ce type de formule en donnant la valeur numérique, cette fois précise, du produit du paramètre de densité par h². Cette quantité, souvent écrite avec la lettre minuscule ω, vaut ici :

.

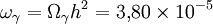
Le fond cosmologique de neutrinos

Le fond cosmologique de neutrinos se présente également sous la forme d'un corps noir. Cette température est cependant inférieure à celle du fond diffus cosmologique, car les neutrinos se sont découplés des photons (c'est-à-dire qu'ils ont cessé d'interagir avec eux) avant que ceux-ci ne se voient injecté de l'énergie lors de l'annihilation électrons-positrons. Le rapport entre les température des photons et des neutrinos primordiaux peut être calculé précisément et vaut, (à une légère correction sans importance près) :

.

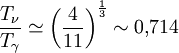
La densité d'énergie se calcule alors, en tenant compte du fait que les neutrinos sont des fermions et non des bosons, et qu'il existe trois espèces de neutrinos et d'anti-neutrinos, mais pour chacune qu'un seul état de spin,

.

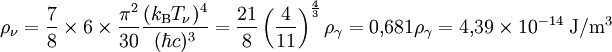
En termes de paramètre de densité, on a alors

.

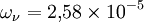
La matière baryonique

L'abondance de matière baryonique est difficile à mesurer directement, car certaines parties de la matière baryonique rayonne beaucoup (celle située dans les étoiles, par exemple), et d'autres moins. D'autre part, le rayonnement de la matière baryonique se fait dans une gamme de longueurs d'ondes variées, du domaine radio aux rayons X, et chacun des processus amenant à interpréter ces rayonnements nécessite une modélisation complexe. Il existe deux méthodes relativement fiables pour estimer la densité d'énergie de la matière baryonique. L'une utilise l'abondance des éléments légers produits lors de la nucléosynthèse primordiale, l'autre la structure des anisotropies du fond diffus cosmologique. Pendant longtemps, seule la première méthode était utilisable, mais c'est désormais la seconde qui est la plus précise. Dans le premier cas, on utilise le fait que la matière baryonique est aujourd'hui non relativiste. De ce fait, sa densité d'énergie n'est rien d'autre que sa densité d'énergie de masse, c'est-à-dire le produit de la densité (ou sa masse volumique moyenne) par le carré de la vitesse de la lumière. De plus, la masse de la matière baryonique est égale au nombre de nucléons (protons ou neutrons) par unité de volume par leur masse moyenne, égale à la masse du proton. On a ainsi

ρ_b = n_bm_pc²,

où m est la masse du proton et n la densité (numérique) de nucléons. Les deux méthodes évoqués ci-dessus estiment en réalité la quantité n, et plus précisément le rapport de celle-ci avec la densité numérique de photons. Cette dernière s'avère être connue, car de même que l'on sait calculer la densité d'énergie d'un corps noir de température donnée, l'on sait calculer sa densité de photons. Un calcul classique donne

,

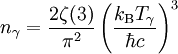
où ζ est la fonction zêta de Riemann pour laquelle on peut évaluer ζ(3) = 1,202, ce qui donne

.

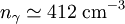
En notant par η le rapport des deux densités numériques de baryons et de photons, on a :

,

.

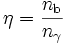
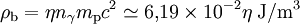
La partie difficile est dans l'évaluation de la quantité η, pour laquelle les deux méthodes ci-dessus donnent une valeur de l'ordre de

,

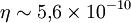
ce qui donne au final

.

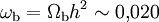
Quelle que soit la valeur exacte de h, il apparaît clairement que le paramètre de densité de la matière baryonique est très significativement inférieur à 1 (de l'ordre de 0,045). La seconde méthode permet, elle de contraindre le rapport ρ_b / ρ_γ non pas aujourd'hui, mais à l'époque de la recombinaison. Ce rapport a part la suite évolué au court du temps, la densité d'énergie baryonique décroissant moins vite que la densité d'énergie des photons. En prenant en compte cette évolution, on retrouve des résultats sensiblement identique, et même plus précis qu'avec la première méthode.

La matière noire