Diviseur (géométrie algébrique) - Définition

Diviseurs de Weil dans une variété.

Variétés projectives propres et lisses.

Les variétés algébriques sur lesquelles on agit généralement sont définies par des combinaisons booléennes d'égalités de polynômes dans l'espace projectif Pⁿ(k). Immergée dans un espace projectif, on suppose que c'en est un fermé, c'est-à-dire une variété elle même projective. Affirmer qu'elle est propre, dans le cas où l'on se place sur (ou l'un de ses sous-corps) revient à dire que l'ensemble de ses points complexes est compact. Enfin, on suppose qu'elle est lisse, c'est-à-dire, dans le cas où il s'agit d'une variété au sens de la géométrie différentielle, que sur chacun de ses composantes connexes, elle possède en tour point un espace tangent de dimension constante.

Les diviseurs de Weil.

Pour une variété irréductible, propre et lisse, on appelle diviseur sur X une somme formelle, à support fini et à coefficients entiers, de sous-variétés fermées et irréductibles, de codimension 1.

Chaque diviseur de Weil s'écrit donc formellement comme une somme finie

où les n_i sont des entiers relatifs, tous nuls sauf pour un nombre fini d'entre eux, les Z_i étant des fermés irréductibles de la variété X.

On appelle effectif tout diviseur dont les coefficients sont positifs.

Cas d'une courbe lisse 

Sur une courbe lisse, et pour un corps algébriquement clos K, un diviseur de Weil est représenté comme une somme formelle de points de cette courbe, y compris le point à l'infini (on se place sur P_1,K). La somme formelle étant prise sur une famille à support fini à valeur dans , et indexée par les points de C(K)

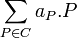
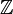
Si le corps n'est pas algébriquement clos, on forme les sommes formelles des places (ou valuations) de la courbe. Un diviseur sur X étant identifié à une combinaison finie,

en prenant un système de représentant des places intervenant dans le diviseur.

quelques propriétés immédiates 

Deux diviseurs sont identiques si les coefficients des deux diviseurs pour tout Z_i sont identiques.

La réunion de deux sous-variétés disjointes s'identifiant à leur somme, on munit l'ensemble des diviseurs d'une loi d'addition coefficient par coefficient.

L'ensemble des diviseurs de Weil forment un groupe abélien pour cette addition formelle.

Degré d'un diviseur.

Cas d'un corps quelconque :

Soit un diviseur écrit au travers d'un système complet de représentants des places de la variété X.

Le degré de D est par définition la somme pondérée

où k(x_i) est le corps résiduel de X en x_i.

On montre que l'application qui à tout diviseur associe son degré est un homomorphisme de groupes à valeurs dans ℤ.

Faisceaux définis sur la variété.

Morphismes 

On définit dessus ces variétés des morphismes, c'est-à-dire, localement des applications définies par des fonctions rationnelles partout définies. On obtient ainsi un premier faisceau, celui des morphismes de la variété.

Diviseurs Principaux 

Si f est une fonction rationnelle non nulle sur X ; c'est-à-dire un morphisme de X vers la droite projective, on lui associe un diviseur qui est différence entre le lieu de ses zéros et le lieu de ses pôles (comptés avec leur multiplicité). On note (f) le diviseur de f. Un tel diviseur est dit principal.

On remarque que (fg) = (f) + (g). On en déduit que l'ensemble des diviseurs principaux de la forme (f) pour f rationnelle sur X forme un sous-groupe du groupe des diviseurs de X.

On montre que la somme des multiplicités d'un diviseur principal est nulle. On dit également que ces diviseurs sont linéairement équivalents à 0.

Par définition, deux diviseurs D et D' sont linéairement équivalents si et seulement si leur différence est un diviseur principal.

Le quotient du groupe des diviseurs par le sous-groupe des diviseurs principaux s'appelle groupe de Picard de la variété X.

sections globales 

On ordonne les diviseurs par la relation : D > D' si et seulement si D − D' est effectif.

Soit D, un diviseur de X, écrit , à la façon de Weil. On considère l'ensemble des fonctions rationnelles f sur X dont le diviseur associé (f) est au moins égal à − D

Celles-ci, possèdent, sur les sous-variétés [x] où ''D'' est positif d'ordre m_[x] des pôles de multiplicité au plus m_[x] et, sur les sous-variétés [x] où ''D'' est négatif, des zéros de multiplicité au moins − m_[x].

Ces fonctions s'appellent les sections globales du faisceau inversible associé au diviseur D.

Faisceaux inversibles 

Le faisceau inversible associé à un ouvert de la variété (au sens de Zariski, c'est-à-dire le complémentaire d'une sous-variété fermée) n'est autre que le faisceau de l'espace vectoriel des sections sur cet ouvert.