Diviseur (géométrie algébrique) - Définition

Introduction

En mathématiques, plus précisément en géométrie algébrique, les diviseurs sont une généralisation des sous-variétés de codimension 1 de variétés algébriques ; deux généralisations différentes sont d'un usage commun : les diviseurs de Weil et les diviseurs de Cartier. Les deux concepts coincident dans les cas des variétés non singulières.

Diviseurs en géométrie algébrique

En géométrie algébrique, comme en analyse complexe, ou en géométrie arithmétique, les diviseurs forment un groupe qui permet de saisir la nature d'un schéma (une variété algébrique, une surface de Riemann, un anneau de Dedekind...) au travers d'un squelette assez simple. Ce groupe provient de l'idée commune aux études menées sur ces objets : on peut connaître une grande part de leur géométrie en étudiant les sous-schémas non triviaux maximaux (sous variétés, ou idéaux de codimension 1).

L'ensemble de ces diviseurs est muni d'une loi de groupe additive. Plusieurs définitions sont possibles, selon le cadre dans lequel on agit. Néanmoins, sous de bonnes conditions, les diviseurs qu'on obtient sont identiques.

On peut agir ainsi dans le cadre de variétés définies sur un corps algébriquement clos ( par exemple) ou sur un corps de nombre quelconque (voire ou les corps p-adiques). On peut les définir sur des structures souples (par exemple des changements de cartes holomorphes) ou plus rigides (variétés algébriques). On peut se placer localement (sur un anneau) ou plus globalement, en regardant toute une surface (et donner alors leur définition à l'aide de faisceau). On peut encore définir les variétés sur lesquelles on veut travailler en termes de schémas, on obtient alors une définition cohomologique des groupes de diviseurs.

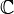
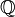
Par bonheur, les deux formes fondamentales de diviseurs, ceux de Weil et ceux de Cartier, coïncident assez souvent.

Diviseurs de Cartier d'une variété irréductible.

Si la variété X est irréductible mais éventuellement singulière, on définit les diviseurs de Cartier, c'est-à-dire, localement, le diviseur des zéros d'une fonction rationnelle. plus précisément :

Les diviseurs de Cartier.

Un diviseur de Cartier peut être représenté comme un recouvrement d'ouverts U_i, associés à une famille de fonctions rationnelles f_i définies sur l'ouvert U_i correspondant ; ces fonctions étant reliées entre elles par les changements de cartes admissibles (inversibles et réguliers) entre ces ouverts de façon à ce qu'elles coïncident (à isomorphismes rationnels multiplicatifs près) sur leur intersection.

En ce sens, un diviseur principal correspond à des fonctions f_i régulières. On peut leur associer les sous-variété de codimension 1 qui en sont les zéros et les pôles.

A chaque diviseur de Cartier, on peut donc associer un diviseur de Weil (tous les anneaux locaux sont factoriels); on obtient ainsi un morphisme injectif entre les deux groupes de diviseurs.

Dans le cas d'une variété projective propre et lisse, il s'agit d'un isomorphisme.

Classes d'équivalence, groupe de Picard.

Les classes d'équivalence des diviseurs de Cartier (modulo les diviseurs principaux) correspondent (de façon injective) aux éléments du groupe de Picard.

Diviseurs de Cartier en termes de faisceaux.

Pour une variété algébrique X, muni des faisceaux O_X des fonctions algébriques sur X , et M_X des fonctions rationnelles sur X. Un diviseur est une section du groupe quotient M ^* / O ^* . L'ensemble de ces sections donnant le groupe des diviseurs de Cartier. On étend ce résultat aux schémas noethériens (dont une variété algébrique est un exemple).

On peut obtient le même résultat en analyse complexe en remplaçant respectivement variété algébrique par variété complexe, algébrique par holomorphes, rationnelles par meromorphes.

A chaque diviseur de Cartier, noté ici ''D'', on peut donc associer une fibre notée O_X(D). La somme des diviseurs correspond alors au produit tensoriel de ces fibres. L'isomorphisme entre fibre correspondant à l'équivalence linéaire des diviseurs de Cartier.

relation entre les diviseurs de Cartier et de Weil.

Si on considère les sections globales du faisceau inversible associé à un diviseur de Cartier, on obtient un injection du groupe des diviseurs de Cartier dans le groupe des diviseurs de Weil.

Par exemple : dans la droite projective, ls diviseur défini par soustraction v_O − v_I,O désignant l'origine et I le point à l'infini, est linéairement équivalent à 0. C'est le diviseur de la fonction

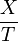
Les groupes de sections de l'un et de l'autre sont isomorphes : Les fonctions ayant éventuellement un pôle simple en zéro étant isomorphes aux fonctions ayant éventuellement un pôle simple à l'infini.

On montre que cette correspondance entre faisceaux inversibles et diviseurs de Cartier est biunivoque.

Si la variété est singulière ces résultats tombent en défaut.

Un exemple de surface sur laquelle les deux groupes sont différents est donné par la quadrique singulière X² + Y² = Z² dans l'espace affine. Une droite passant par le sommet est un diviseur de Weil qui ne correspond à aucun diviseur de Cartier.