Diviseur (géométrie algébrique) - Définition
La liste des auteurs de cet article est disponible ici.
Le langage des anneaux.
Weil en termes d'anneaux.
Si A désigne un anneau, on appelle diviseur de Weil une combinaison linéaire à coefficients entiers de quotients A / p de l'anneau A par des idéaux premiers P tels que dim(AP) = 1.
Si n est un entier, un cycle de codimension n, noté Zn(A) est une combinaison linéaire de type
![\sum_{i=1}^n n_i.[A/p_i]](https://static.techno-science.net/illustration/Definitions/autres/8/89241e6715c1fa9422b88eab227a916d_f6c9827d3497ba18a82712e388dd153e.png)
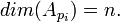
Ainsi les diviseurs de Weil sont les cycles de codimension un.
Exemple :
Si I est un idéal de A et A un anneau noetherien ; si dim(A / p) / geqn pour tout idéal premier de I, on peut lui associer un cycle de codimension n ; noté cycle(A / I)A et défini par :
![cycle(A/I) A=\sum_{ dim A_p=n }long((A/p)/(IA/p))[A/p]](https://static.techno-science.net/illustration/Definitions/autres/d/dada60addf5b1fee8e72372b61cbb423_925b4acbb8a057fe4794376713012d63.png)
La somme étant finie.
Lorsque I est un A-module inversible (c'est-à-dire, si I est localement engendré par un élément non diviseur de zéro) on obtient un diviseur de Weil. On note Z1(A) leur ensemble.
Cartier en termes d'anneaux.
Soit A un anneau. On appelle groupe des diviseurs de Cartier de A, et on note Div(A) le groupe engendre par le monoïde des idéaux (A-modules) inversibles.
On voit que si I et J sont deux idéaux dans Div(A) alors
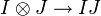
Si A est un anneau de Dedekind l’application cycle :
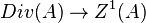
Diviseurs principaux, groupe de Picard.
- Définition
Toujours sur un anneau, noté A. On appelle diviseurs principaux de A, et on note Pr(A) le sous-groupe de Div(A) engendre par les idéaux fA où f est non-diviseur de zéro. Ce groupe est canoniquement isomorphe `a K * / A
Si A, est un anneau de Dedekind, K, son corps de fractions et f, un élément de K, alors
![(f) =\sum dim A/p= vp(f)[A/p]](https://static.techno-science.net/illustration/Definitions/autres/4/47c776b0de4a470fbd691d9830884495_2106261b82021a4b5476dd860a4803b7.png)
- Proposition
Avec les notations introduites ci-dessus si A est intègre on a la suite exacte :
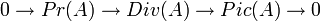
Diviseurs remarquables.
- Le diviseur canonique
Pour les courbes sur un corps k, algébriquement clos. On considère une fonction non constante, f, définie sur X. la forme différentielle df sur X s'écrit en tout point
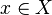
On appelle l'ordre de df, et on le note vx(df) l'ordre de g en x.
On considère alors le diviseur
![(df):=\sum_{x\in X}v_x(df)[x]](https://static.techno-science.net/illustration/Definitions/autres/f/f7e25b38477367271c16307abb516563_4c3efccbcc16824bb0920b93b255b684.png)
Cette nomination étant justifié par le fait que pour une autre fonction rationnelle, le diviseur canonique associés est linéairement équivalent au premier. Ainsi, le diviseur canonique apparaît pour sa part comme un élément du groupe de Picard.
- Diviseur à l'infini , faisceaux amples
Un diviseur de l'espace projectif, est défini par l'hyperplan à l'infini (avec multiplicité 1).
À équivalence linéaire près, il est équivalent au diviseur défini par n'importe quel hyperplan.
On note O(1) le faisceau de ses sections (ou faisceau inversible associé). Ce faisceau est appelé le faisceau de Serre : une section de O(1) est une fonction rationnelle qui a au plus un pôle simple (à l'infini ou ailleurs)
Un faisceau inversible est dit très ample lorsqu'on peut plonger la variété comme une variété fermée dans un espace projectif de façon que le diviseur (associé au faisceau) soit l'intersection de la variété avec le diviseur défini ci-dessus
Un faisceau ample est un faisceau dont une certaine puissance tensorielle (positive) est très ample.
Une condition (CNS) pour qu'un faisceau soit ample est que le degré du diviseur associé soit strictement positif.

















































