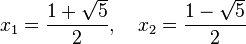Équation du second degré - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une équation du second degré, encore appelée équation quadratique se présente sous la forme suivante :
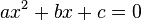
les lettres a, b et c désignent des nombres, et a est, par définition, différent de 0. La lettre x désigne l'inconnue. Le terme de second degré provient du fait que le polynôme définissant l'équation est du second degré.
Deux identités remarquables permettent de trouver les éventuelles solutions. Il en existe entre zéro et deux (éventuellement confondues), si les solutions recherchées sont des nombres réels. Le calcul du discriminant permet de connaître le nombre exact de solutions et offre une méthode synthétique de résolution.
Dans le cas où les solutions recherchées sont des nombres complexes, il existe toujours deux solutions, elles peuvent néanmoins être confondues.
Éléments clé
Introduction par l'exemple
On recherche les éventuelles solutions de l'équation suivante :
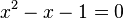
Le terme de gauche est appelé trinôme du second degré. Il est composé de trois termes, tous de la même forme : un nombre non nul que multiplie une puissance entière de x. Chaque terme est appelé monôme et, comme il en existe trois, on parle de trinôme. La plus grande puissance de ces monômes est deux, pour cette raison, on parle de second degré. L'expression 0.x2 + x + 1 n'est pas un trinôme, car l'un des nombres est nul. L'expression s'écrit encore x + 1, on parle de binôme du premier degré.
La méthode consiste à forcer l'apparition d'une première identité remarquable. On écrit le polynôme de la manière suivante :
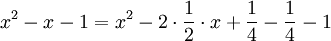
Les trois premiers termes sont ceux d'une somme remarquable. L'application d'une identité remarquable permet d'écrire le polynôme de la manière suivante :
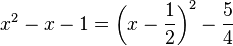
Un peu d'imagination permet d'appliquer une deuxième identité remarquable :
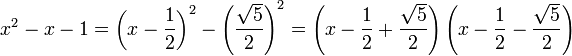
L'équation initiale s'exprime alors sous forme d'un produit de deux facteurs :
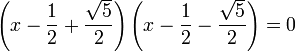
Un produit de deux facteurs est nul si, et seulement si, l'un des facteurs est nul. Cette remarque permet de trouver les deux solutions x1 et x2 :
|
|
Cette équation n'admet qu'une unique racine positive x1, cette valeur est appelée nombre d'or. Il est aussi possible de résoudre une équation du second degré sans la moindre connaissance d'algèbre, le paragraphe Méthode géométrique montre comment s'y prendre.
Discriminant
On considère l'équation suivante, où a, b et c désignent des nombres réels et a est différent de 0 :
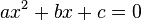
On dispose de la définition suivante:
Définition du discriminant — Le discriminant de l'équation est la valeur Δ définie par :
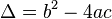
Cette définition est la source du théorème associé à la résolution de l'équation du second degré, dans le cas où l'on recherche des solutions réelles:
Résolution de l'équation — Si le discriminant est strictement positif, l'équation admet deux solutions x1 et x2 données par les formules suivantes :
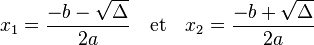
Si le discriminant est nul, l'équation admet une racine double :
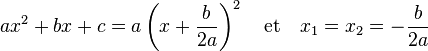
Si le discriminant est strictement négatif, l'équation n'admet pas de solution réelle.
Interprétation graphique
Une manière d'étudier l'équation du paragraphe précédent est de considérer la fonction f de la variable réelle et à valeurs réelles définie par :
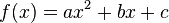
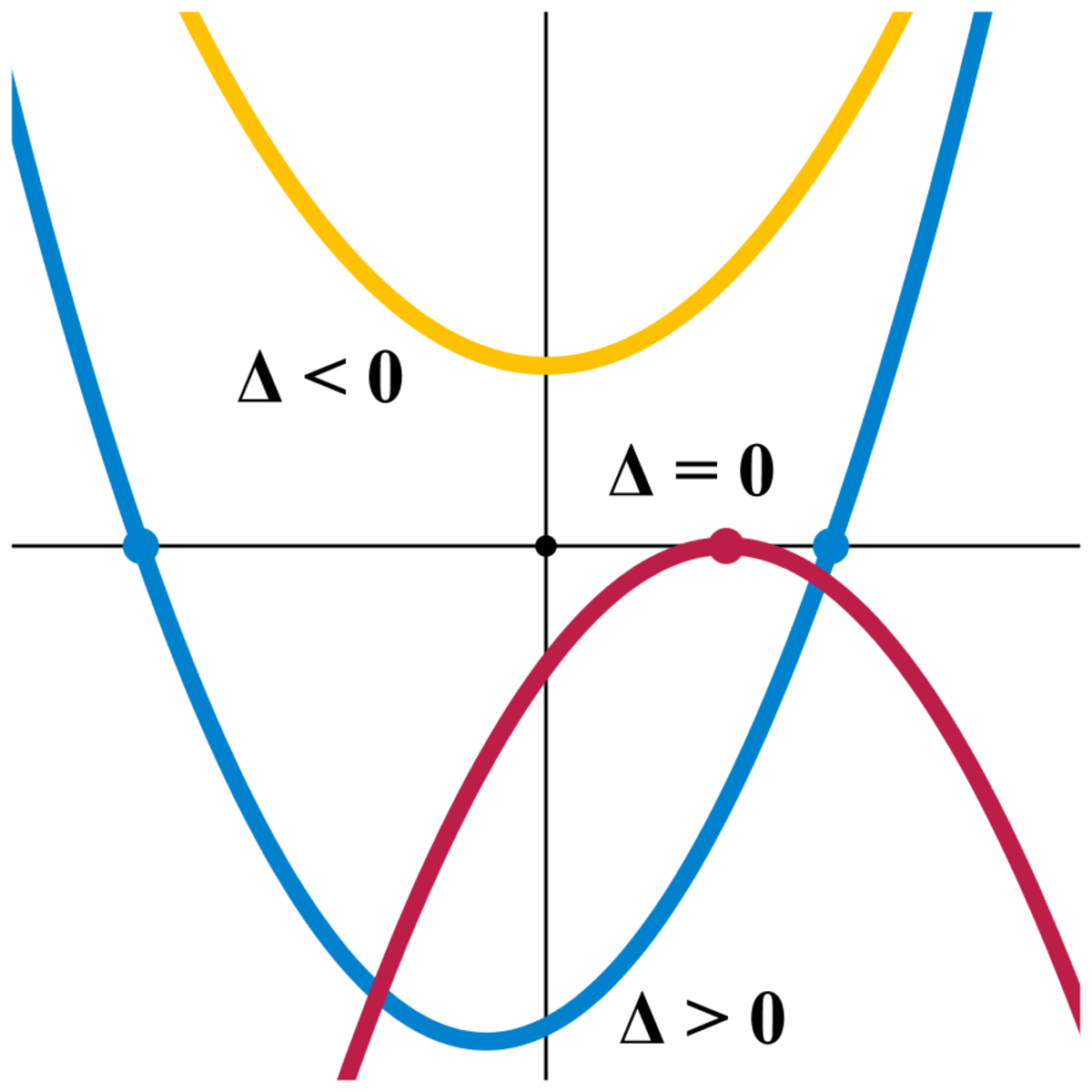
L'équation peut encore s'écrire f(x) = 0. Les solutions de l'équation sont les abscisses des points d'intersection du graphe de la fonction f et de l'axe des x. Le graphe de la fonction f est appelé une parabole, elle possède une forme analogue à celle des trois exemples présentés à droite. Si a est positif, les branches de la parabole sont dirigées vers le haut, comme pour les exemples jaunes ou bleus, sinon les branches sont dirigées vers le bas, comme l'exemple rouge.
Si le discriminant est strictement positif, comme pour l'exemple bleu, cela signifie que le graphe de f croise l'axe des abscisses en deux points. Si le discriminant est nul, la configuration est celle de la parabole rouge, le graphe se situe soit dans le demi-plan des ordonnées positives soit dans le demi-plan des ordonnées négatives et son unique extremum est sur l'axe des abscisses. Dans le cas d'un discriminant strictement négatif, comme pour la parabole jaune, le graphe se situe encore dans l'un des deux demi-plans précédents, mais cette fois l'extremum ne rencontre pas l'axe des abscisses.
Ainsi, si le discriminant est strictement positif, le signe des valeurs que prend la fonction f entre les solutions est l'opposé du signe des valeurs prises par f à l'extérieur du segment d'extrémités les solutions de l'équation.