Équation du second degré - Définition

Historique

Les problèmes du second degré se posaient chez les Babyloniens (on cherchait alors une solution positive à l'aide d'un algorithme : voyez les explications à propos de la tablette Plimpton 322), chez les Égyptiens, voire chez les Grecs (Livre II des Éléments d'Euclide), mais aucune civilisation de cette époque n'a explicitement étudié les équations.

Les équations du second degré ont été les premières équations résolues, l'équation mathématique est inventée en même temps que l'algèbre par le savant iranien musulman Al-Khwarizmi au IX^e siècle, qui reprit cette tradition, augmentée des connaissances grecques pour la démonstration, afin de trouver une solution (réelle et positive). Les équations étaient présentées sous l'une des formes suivantes parce qu'un nombre était supposé positif :

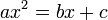
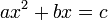
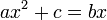
La résolution utilise des méthodes simples comme le théorème de Pythagore, essentiellement fondées sur la géométrie du triangle et du carré. Elle est explicitée dans l'article algèbre géométrique.