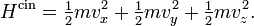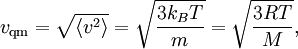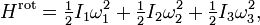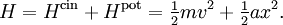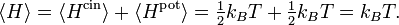Équipartition de l'énergie - Définition

Première approche

Dans une première approche, on résume souvent le théorème d’équipartition de la façon suivante :

Cet énoncé n’est qu’un résultat particulier du théorème. Il omet certaines hypothèses. Cependant, il permet déjà de retrouver un certain nombre de résultats et de traiter des cas particuliers importants qui sont détaillés ci-dessous. Bien entendu, on retrouve dans cette affirmation le fait que l’énergie est répartie également entre tous les degrés de liberté, d’où le nom « équipartition ».

Dans la suite, le symbole H, pour Hamiltonien, sera utilisé comme symbole pour l’énergie en raison du rôle central que joue le formalisme de Hamilton dans la formulation plus générale du théorème d’équipartition qui suivra. D’autre part, on notera avec des crochets la valeur moyenne d’une quantité X. On en précisera par la suite le sens mathématique précis.

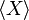
Gaz parfait monoatomique : l’exemple des gaz rares

Les gaz rares sont des exemples types pour l’application du théorème d’équipartition. Comme on le voit sur cette simulation, la vitesse, et donc l’énergie cinétique d’un atome donné, peut fluctuer considérablement. Le théorème d’équipartition permet de calculer son énergie cinétique moyenne à une température donnée. Dans ce schéma, cinq particules ont été colorées en rouge afin de suivre plus facilement leur mouvement. La couleur n’a pas d’autre signification.

Un gaz rare est un gaz des plus simples qui soient : il est constitué uniquement d’atomes dont l’énergie n’est donc composée que de l’énergie cinétique due à leur mouvement de translation. Chaque atome dispose de trois degrés de liberté associés aux trois composantes de la vitesse, c’est-à-dire aux trois directions de l’espace. Si on décompose la vitesse de l’atome suivant ces trois directions en les notant v_x, v_y et v_z, en notant m la masse, alors l’énergie cinétique (newtonienne) s’écrit comme une somme de trois termes dont chacun correspond à un degré de liberté :

À l’équilibre thermodynamique, chaque degré de liberté contribue d’après le théorème d’équipartition pour 1/2 k_BT à l’énergie cinétique. L’énergie cinétique moyenne totale d’une particule est donc 3/2 k_BT, et l’énergie totale d’un gaz parfait composé de N particules est 3/2 Nk_BT.

Il s’en suit que la chaleur spécifique du gaz est 3/2 Nk_B et donc en particulier que la chaleur spécifique d’une mole d’un tel gaz est 3/2 N_Ak_B où N_A est le nombre d’Avogadro, ou encore 3/2 R où R est la constante des gaz parfaits. Puisque R vaut approximativement 2 cal/(mol.K), le théorème prédit que la capacité thermique molaire d’un gaz parfait est environ 3 cal/(mol.K).

Connaissant l’énergie cinétique moyenne, on peut calculer la vitesse quadratique moyenne v_qm des atomes du gaz :

où M = mN_A est la masse d’une mole de gaz. La vitesse quadratique moyenne est donc d’autant plus faible que les atomes sont lourds. Les atomes du xénon auront une vitesse moyenne plus basse que les atomes plus légers de l’hélium à une même température. Ce résultat est utile dans un grand nombre d’applications, telles que la loi d’effusion de Graham dont a été tirée notamment une méthode d’enrichissement de l’uranium.

Gaz parfait diatomique et polyatomique

On considère maintenant un gaz dont les molécules sont composées de deux atomes ou plus. On suppose que les différents atomes sont liés rigidement entre eux. Une telle molécule dispose comme dans le cas précédent de trois degré de libertés associés à son déplacement dans le conteneur. Mais elle peut aussi tourner sur elle-même et accumuler ainsi de l’énergie. Ces degrés de libertés supplémentaires contribuent aux aussi à l’énergie totale et à la chaleur spécifique.

Dans le cas le plus général, si les moments d’inertie principaux de la molécule sont I₁, I₂ et I₃, alors cette énergie cinétique de rotation est donnée par

où ω₁, ω₂ et ω₃ sont les composantes principales de la vitesse angulaire. Ce cas est formellement très similaire au cas précédent ; l’énergie est proportionnelle au carré de la vitesse angulaire. Par un raisonnement identique, l’équipartition implique donc que l’énergie cinétique moyenne de rotation de chaque molécule est 3/2 k_BT à l’équilibre.

Il convient de distinguer deux cas, selon que la molécule est linéaire (atomes parfaitement alignés) ou non. Dans le premier cas, la molécule ne peut pas accumuler de l’énergie par rotation autour de son axe : il n’y a que deux degrés de liberté au lieu de trois. La contribution de l’énergie cinétique de rotation à l’énergie totale sera deux fois 1/2 k_BT seulement. Pour une molécule non linéaire, l’énergie moyenne totale de rotation est en revanche 3/2 k_BT.

Dans les gaz diatomiques tels que l’azote, l’oxygène, les molécules sont composées de deux atomes identiques et sont forcément linéaires. Avec le modèle de molécule que l’on vient de décrire, la chaleur spécifique totale d’un tel gaz diatomique est donc 5/2 R.

Vibration des molécules

Modes de vibration d’une molécule de CO₂. Chaque mode contribue comme un oscillateur harmonique pour k_BT à l’énergie totale du gaz. Le 4^e mode, identique au (c) à une rotation près, n’est pas représenté ici.

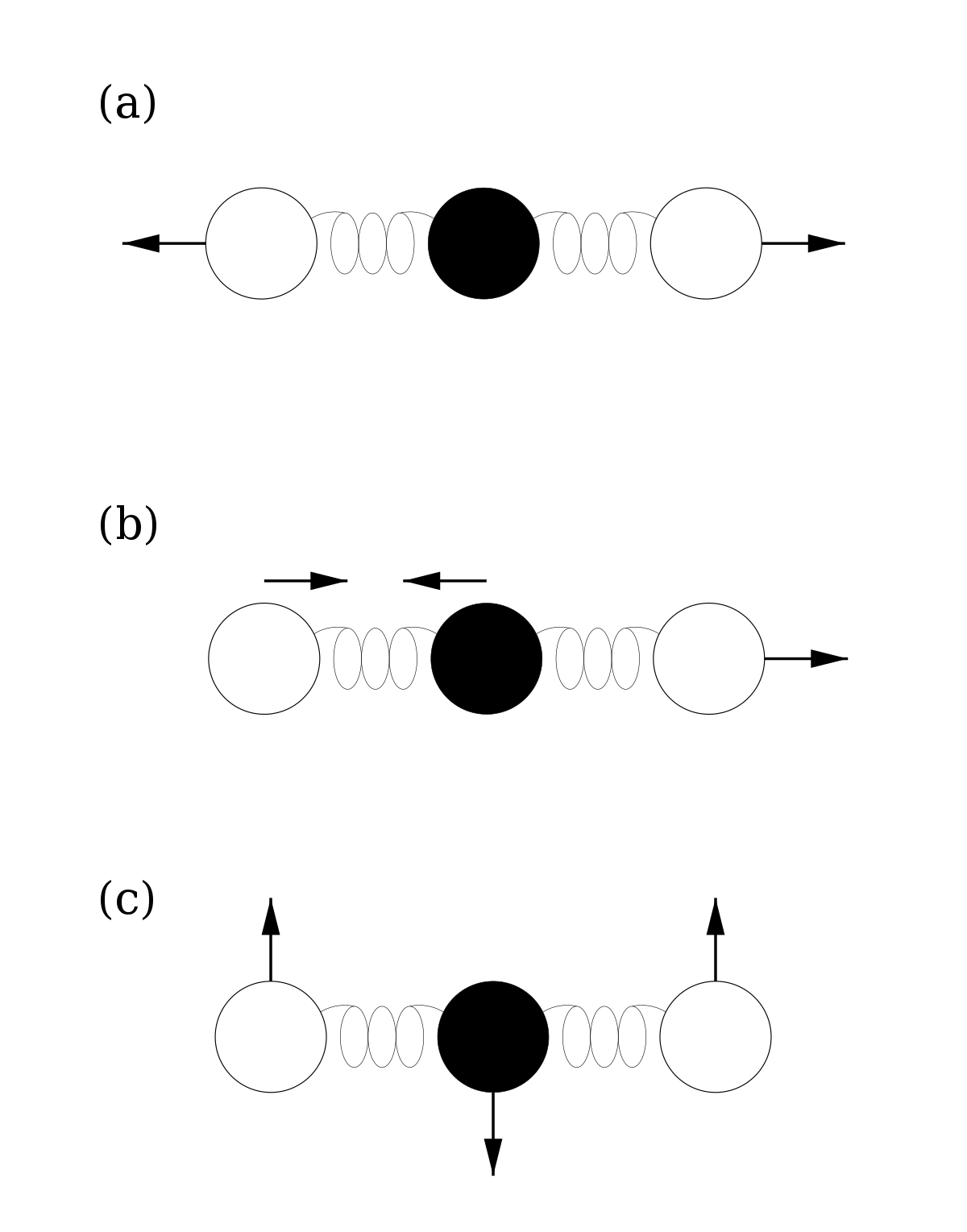
Si on considère qu’une molécule de gaz est un ensemble de plusieurs atomes liés élastiquement et non plus rigidement, alors cette molécule peut vibrer et accumuler de l’énergie dans son mouvement de vibration. On peut alors modéliser un mode de vibration de la molécule par un oscillateur harmonique. Dans le cas le plus simple à une dimension, cet oscillateur a a deux types d’énergie :

• de l’énergie cinétique, fonction de sa masse m et sa vitesse v
• de l’énergie potentielle associée à la force de rappel qui tend à le ramener vers sa position d’équilibre. Cette énergie est fonction de la raideur du ressort a et de l’écart à la position d’équilibre x.

L’énergie totale est alors obtenue en additionnant ces deux énergies :

Le théorème d’équipartition s’applique de la même manière aux deux composantes de l’énergie, chacune comptant pour un degré de liberté. À l’équilibre, l’oscillateur aura donc une énergie moyenne

Chaque oscillateur, donc chaque mode de vibration, a donc une énergie moyenne totale k_BT et contribue pour k_B à la chaleur spécifique du système. Pour connaître la contribution des vibrations moléculaires à l’énergie totale, il suffit donc de connaître le nombre de ses modes propres de vibrations : une molécule composée de n atomes en possède 3n − 5 si tous les atomes sont alignés comme dans le CO₂ représenté ci-contre, et 3n − 6 dans le cas contraire, par exemple pour la molécule d’eau.

On verra dans la suite qu’il faut toutefois être prudent : tous les modes ne contribuent pas nécessairement à l’énergie totale selon la température ; la mécanique quantique permettra d’expliquer pourquoi.