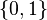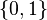Espace topologique - Définition

Limite

Adhérence

Cette notion est développée dans un article spécifique Adhérence. Nous ne développerons cette notion que dans la mesure où elle est nécessaire pour formaliser la notion de limite.

En topologie, l'adhérence d'une partie X d'un espace topologique est le plus petit ensemble fermé qui contient cette partie. On la note souvent . Elle vérifie les propriétés :

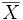
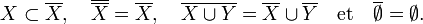
Inversement, étant donné un ensemble E, toute application qui vérifie ces quatre propriétés (appelées Axiomes de fermeture de Kuratowski) permet de définir sur E une topologie, en décrétant que les fermés de cette topologie sont les tels que (et que les ouverts sont les complémentaires des fermés).

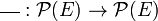
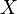
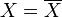
En termes d'adhérences, une application d'un espace topologique dans un autre est continue si et seulement si l'image d'un point adhérent à une partie est nécessairement adhérente à l'image de cette partie.

Définition

La notion de limite en un point, si elle existe, décrit le comportement qu’une fonction "devrait avoir" si elle était définie en ce point. L’exemple le plus simple est le cas d’une fonction définie sur un intervalle ouvert de  ; la limite est le concept qui permet de déterminer le comportement de la fonction aux bornes de cet intervalle.

Soit et deux espaces topologiques. Soit un sous-espace de muni de sa topologie induite et une fonction de dans . Soit enfin un point de et un point de . Alors est la limite de la fonction au point si et seulement si l’image réciproque d’un ouvert contenant contient un ouvert de contenant . Cet énoncé est équivalent à celui qui est donné dans l’article voisinage. L’énoncé étant plus simple avec le formalisme des voisinages, c’est en général celui-là qui est utilisé.

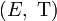
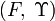
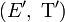
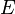
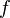
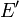
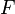
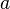
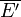
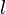
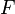
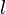
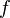
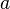
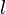
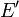
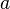
Remarque 1 

La notion de limite est développée dans les articles Limite (mathématiques) et Limite (mathématiques élémentaires).

Remarque 2 

Si le point est élément de l’ensemble , alors la limite, si elle existe, est égale à et la fonction est continue en .

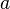
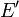
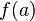
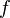
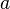
Applications continues

Définitions

Un des premiers intérêts de la notion d'espace topologique est de pouvoir définir une application continue. Il existe deux approches, l'approche locale donnée dans l'article voisinage et qui définit la continuité en un point, et l'approche globale qui définit la continuité en tout point.

• Définition globale. Une application de entre deux espaces topologiques est dite continue si l'image réciproque de tout ouvert de est un ouvert de (l'image réciproque est l'ensemble de tous les points de que envoie dans ).

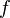
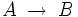
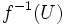
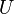
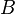
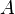
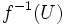
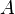
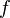
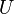
• Définition locale. Soit une fonction d'un espace topologique dans et soit un point élément du domaine de définition de . La fonction est continue au point si et seulement si l'image réciproque d'un ouvert contenant contient un ouvert contenant . Cet énoncé est équivalent à celui donné dans l'article voisinage.

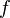
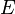
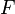
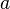
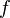
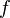
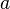
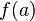
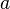
• Équivalence de la continuité locale en tout point et de la continuité globale. Si une application est globalement continue, l'image réciproque d'un ouvert contenant contient elle-même qui est un ouvert contenant . L'application est donc continue en tout point. Réciproquement, si l'application est continue en tout point alors son image réciproque contient pour chaque point un ouvert le contenant et inclus dans l'image réciproque. L'union de tous ses ouverts est par définition un ouvert et est égal à l'image réciproque. L'image réciproque est donc ouverte.

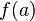
Une application bijective continue et dont la réciproque est continue est appelée un homéomorphisme.

Exemples

• L'application identité d'un espace topologique dans lui-même est continue. En effet l'image réciproque de tout ouvert est lui-même donc est ouvert.

• Une application constante d'un espace topologique dans un autre est continue. En effet l'image réciproque est soit l'ensemble vide soit l'ensemble de départ tout entier.

• l'application est continue. La preuve en est donnée dans l'article continuité.

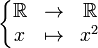
• Soit un espace X munie d'une topologie, , quelconque, on le notera . On appelle X muni de la topologie discrète, , et de la topologie grossière, . Alors il existe les bijections continues (dont l'inverse n'est pas continue, sauf exceptions) . La première étant d'inverse continu quand ( ) et la seconde quand ( ).

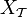
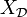
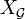
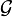
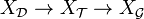
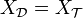
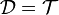
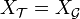
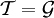
• Soit l'espace de Sierpinski Ω (le couple {0,1} muni de la topologie ). Soit X un espace topologique, alors pour chaque fonction continue de X dans Ω on a un ouvert de X donné par l'image réciproque de {1} et pour chaque ouvert de X une fonction continue de X dans Ω qui vaut 0 sur le complémentaire de l'ouvert et 1 sur l'ouvert. On obtient ainsi une bijection entre les fonctions continues de X dans Ω et les ouverts de X.

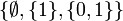
• Même exemple que juste au-dessus, mais on munit le couple et X de leurs topologies discrètes. Ainsi on a une bijection entre les parties de X et les fonctions continues de X dans .