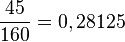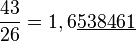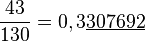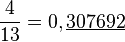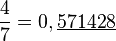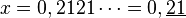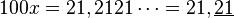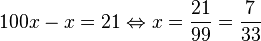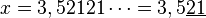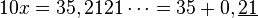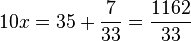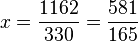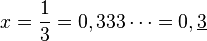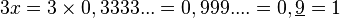Développement décimal périodique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématiques, le développement décimal périodique d'un nombre rationnel est une écriture qui explicite la suite des décimales de ce nombre, en indiquant un bloc de chiffres qui se répète à l'infini. Ce bloc, ou période, peut être constitué d'un ou plusieurs chiffres, un même chiffre pouvant apparaître plusieurs fois dans ce même bloc. Les décimales de ce bloc de chiffres sont parfois appelées décimales récurrentes.
Exemple introductif
Pour évaluer le quotient 4/3, une calculatrice affiche usuellement le chiffre 1, un séparateur décimal (point ou virgule) et plusieurs chiffres 3. Or 1,333333333333 n'est qu'une valeur approchée (à 10 − 12 près) de ce quotient, comme le montre le calcul de l'opération réciproque :
-
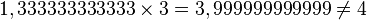
L'algorithme de division appliqué à cet exemple produit à chaque étape le reste 1 qui, multiplié par 10 et divisé par 3, produit le quotient entier 3 et à nouveau un reste 1.
Pour écrire exactement le quotient 4/3 en notation décimale, il faudrait donc répéter le chiffre 3 à l'infini. Pour d'autres nombres rationnels, il faut répéter d'autres chiffres, voire un bloc de plusieurs chiffres. Ces blocs peuvent aussi être précédés par un bloc d'une ou plusieurs décimales qui ne se répète pas.
Développement périodique et nombre rationnel
Écriture décimale d'un rationnel
Dans l'idée de convertir un nombre rationnel représenté sous forme de fraction en forme décimale, on peut poser une division. Par exemple, considérons le nombre rationnel 5/74 :
| 5, | 0 | 0 | 0 | 0 | 0 | 0 | 74 |
| 4 | 4 | 4 | 0,06756... | ||||
| 5 | 6 | 0 | |||||
| 5 | 1 | 8 | |||||
| 4 | 2 | 0 | |||||
| 3 | 7 | 0 | |||||
| 5 | 0 | 0 |
etc. On observe qu'à chaque étape,il y a un reste ; les restes successifs affichés ci-dessus sont 56, 42 et 50. Lorsque on arrive au reste 50 et qu'on abaisse le « 0 », on divise à nouveau 500 par 74. C'est le même problème par lequel on a commencé. Par conséquent, les décimales se répètent : 0,0675675675... Le résultat est prévisible. Les seuls restes possibles — dans ce cas il y en a 74 — sont : 0, 1, 2, ... et 73. Dès que l'on retombe sur un reste déjà obtenu, la séquence entière se répète.
Cet exemple met en évidence la propriété suivante:
Écriture décimale — Tout quotient de deux entiers possède une écriture décimale finie ou périodique
Si le quotient est mis sous forme irréductible, c'est-à-dire sous la forme
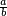
Exemples
Le développement décimal est fini ou périodique. Quand on pose la division de a par b, à chaque étape, il n'y a que b restes possibles car le reste est toujours strictement inférieur au quotient. La division s'arrête au premier reste nul. S'il existe un reste nul, le quotient a alors une écriture décimale finie. Si cela n'est pas le cas, on pose a = bN + r0 et on effectue les divisions successives de 10rk par b, donnant pour quotient ak + 1 et pour reste rk + 1. Le quotient
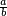
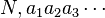
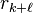
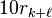
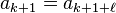
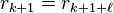
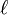
Si b est un produit de puissance de 2 et de 5 alors le quotient est un décimal. Si b = 2k5m, alors
La longueur de la période est inférieure ou égale à b - 1. Les deux restes ont été trouvés lors des b premières étapes donc k + ℓ est inférieur ou égale à b - 1 (première étape: calcul de r0) et
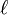
La longueur de la période ne dépend que de b. Si

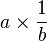

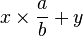
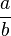
Si b et 10 sont premiers entre eux, la période commence juste après la virgule.Les différents restes ri sont les restes de la division euclidienne de 10ir0 par b. Si
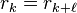
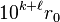
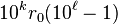
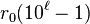
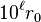
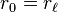
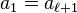
Écriture fractionnaire d'un développement périodique
Pour le développement périodique d'un nombre plus petit que 1, lorsque la période commence immédiatement après la virgule, la technique consiste à multiplier le nombre par la bonne puissance de 10 permettant de décaler complètement la période avant la virgule. Une soustraction permet alors de faire disparaître la partie décimale.
Exemple :
Si la période ne commence pas juste après la virgule, il faut commencer par multiplier le nombre par la bonne puissance de 10 pour faire démarrer le développement décimal périodique juste après la virgule, puis on utilise la méthode précédente sur la partie décimale.
Exemple :
Cet algorithme se généralise et conduit au résultat suivant :
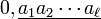
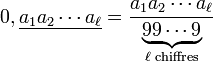
Le cas des nombres décimaux
Un nombre décimal est un nombre qui admet un développement décimal limité, c'est-à-dire ne comportant qu'un nombre fini de décimales autres que zéro.
La méthode de calcul des fractions à partir des décimales répétées, par exemple, dans le cas de 0,9999...=0,9 conduit à un paradoxe apparent :
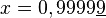
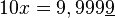
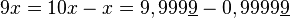
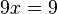
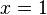
L'égalité 1= 0,999... est parfois contestée de façon naïve. Un bon argument est que si deux nombres réels sont distincts, alors il existe une infinité d'autres nombres réels entre les deux (strictement). Or, il n'existe aucun autre réel entre 0,99999 (une infinité de 9) et 1. C'est donc un seul et même réel, écrit de deux manières différentes.
Certains argumentent que, dans la seconde étape ci-dessus, 10.x vaut 9,9999...0 et non 0,999. Mais ce n'est pas le cas ; le second membre ne se termine pas (il est récurrent) et donc il n'y a pas de fin pour laquelle un zéro peut être trouvé.
L'écriture de 1 sous forme 0,9999... pose le problème de l'unicité de l'écriture décimale d'un nombre. L'écriture sous forme 0,999.... est alors considérée comme un développement décimal impropre. Mais cela ne signifie pas que l'on ne soit jamais amené à l'écrire. En effet, le travail sur l'écriture décimale de 1/3, par exemple, conduit aux égalités :
Ou encore, lorsqu'il s'agit de déterminer le développement décimal de 1 - x, connaissant celui de x, la forme 0,999... est plus adaptée:
- x = 0,52121...= 0,521
- 1- x = 0,99999...- 0,52121...= 0,47878...=0,478
Pour d'autres preuves de cette égalité, voir l'article Développement décimal de l'unité. Le raisonnement mené sur cet exemple peut l'être sur tout autre nombre décimal et donc en particulier tout nombre entier. La conclusion étant :
Développement décimal périodique d'un nombre décimal — Tout nombre décimal admet deux développements décimaux périodiques : l'un dont la période est 9, l'autre dont elle est 0.