Solide de Platon - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie euclidienne, un solide de Platon est un polyèdre régulier convexe. Entre les polygones réguliers convexes de la géométrie plane et les polyèdres réguliers convexes de l’espace à trois dimensions, il y a une analogie, mais aussi une différence notable. De tels polygones sont en nombre infini, leur nombre de côtés est n’importe quel nombre entier supérieur ou égal à trois, alors qu’il existe seulement cinq polyèdres réguliers convexes : cinq solides de Platon.
| Les cinq polyèdres réguliers convexes (solides de Platon) | ||||
|---|---|---|---|---|
| Tétraèdre | Hexaèdre ou Cube | Octaèdre | Dodécaèdre | Icosaèdre |
 | 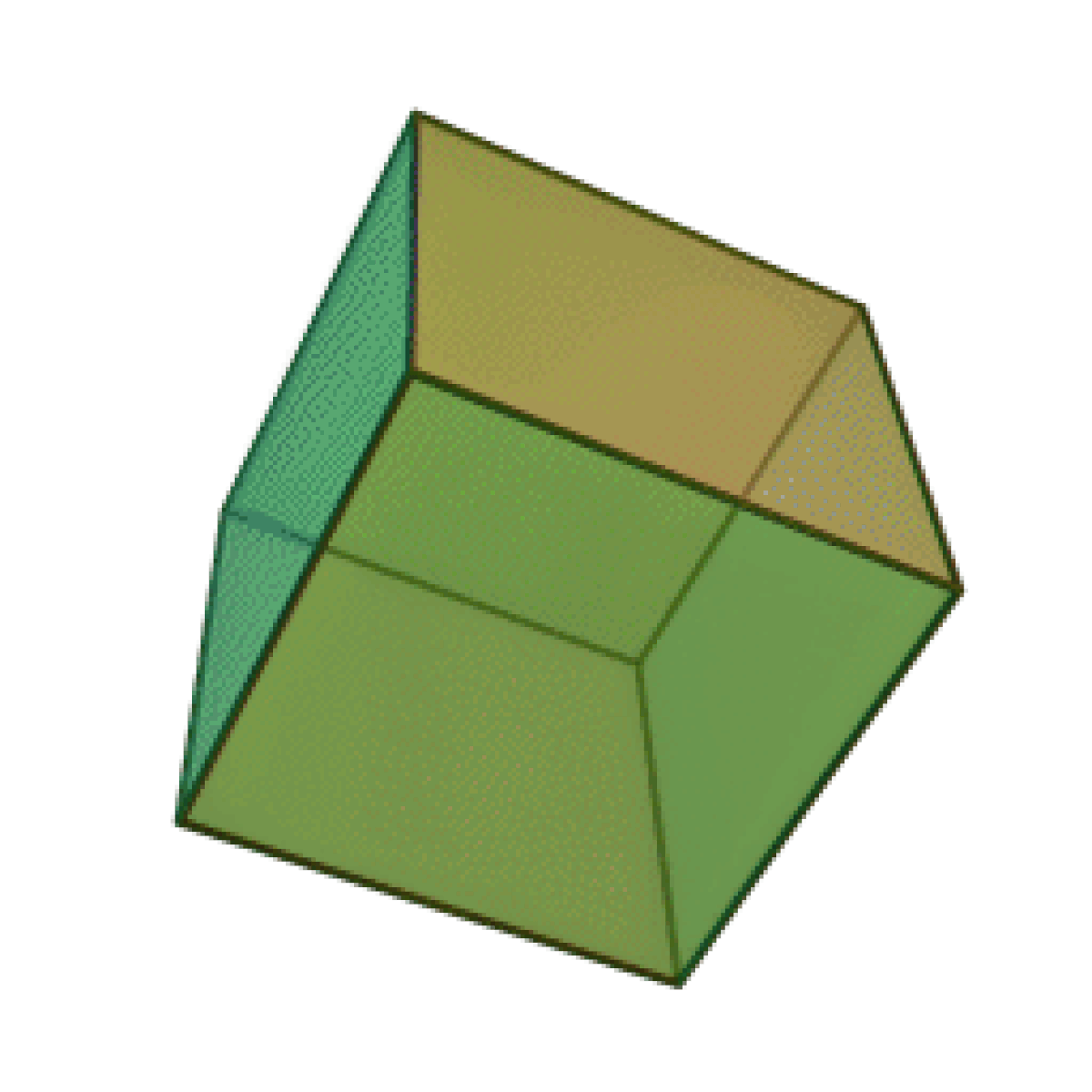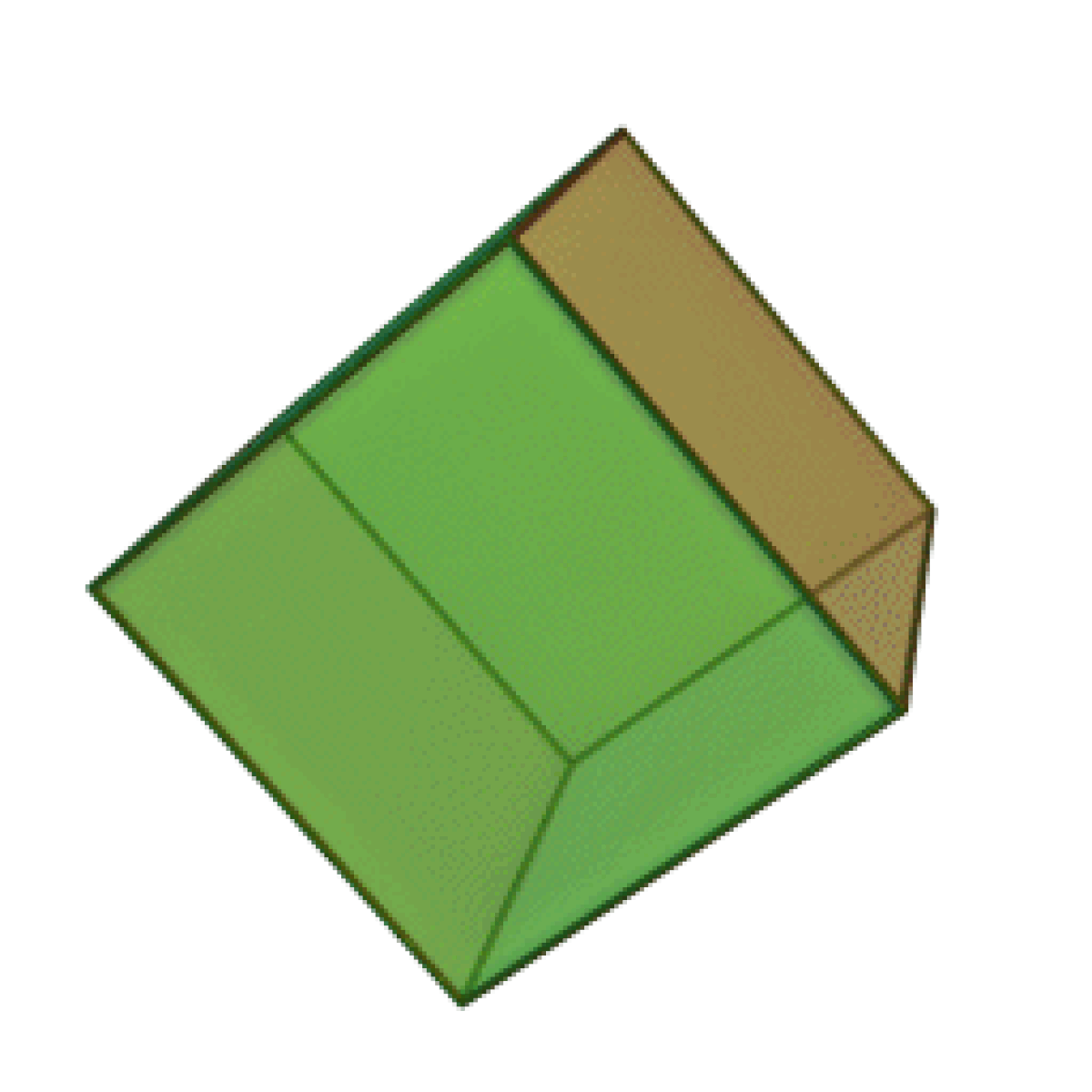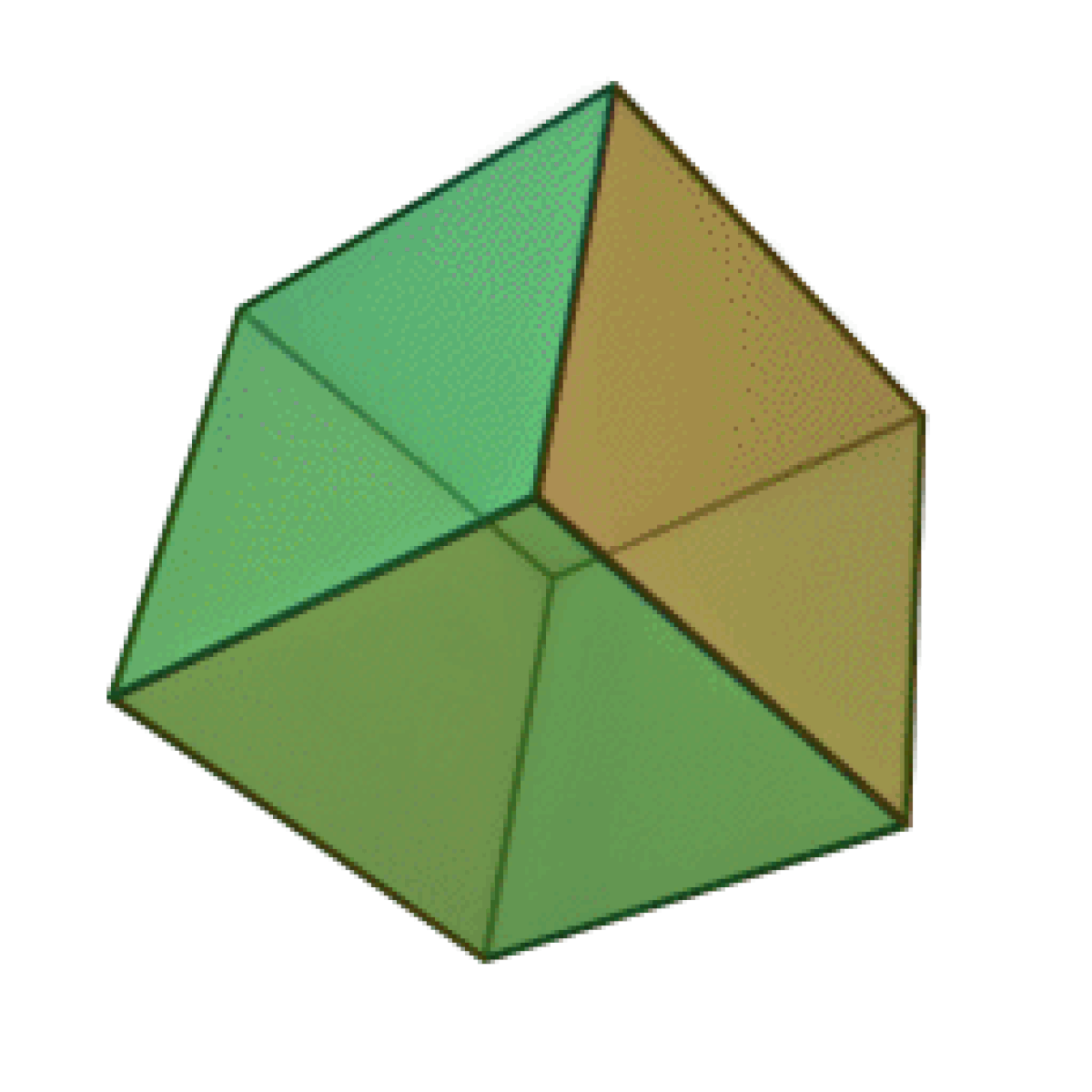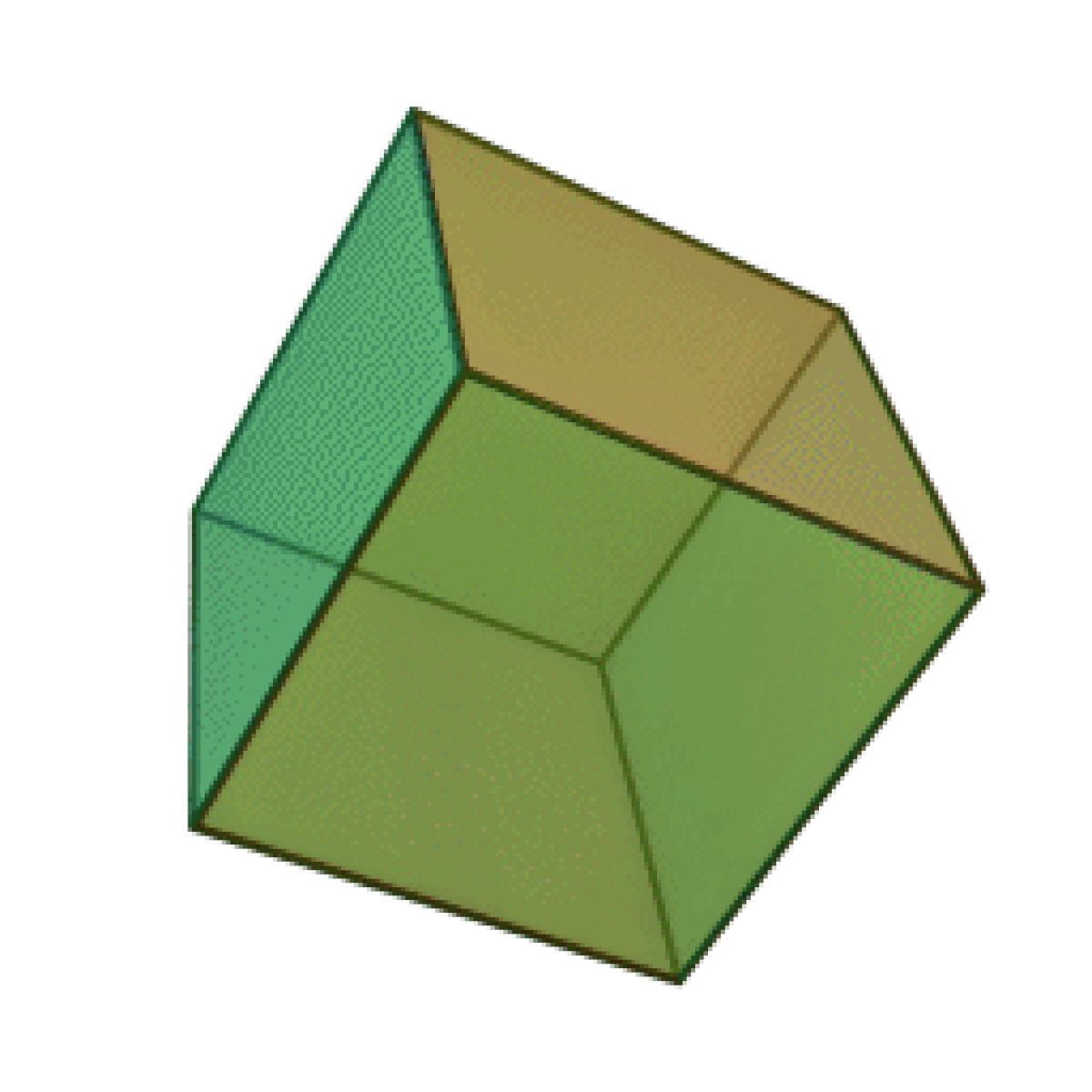 | 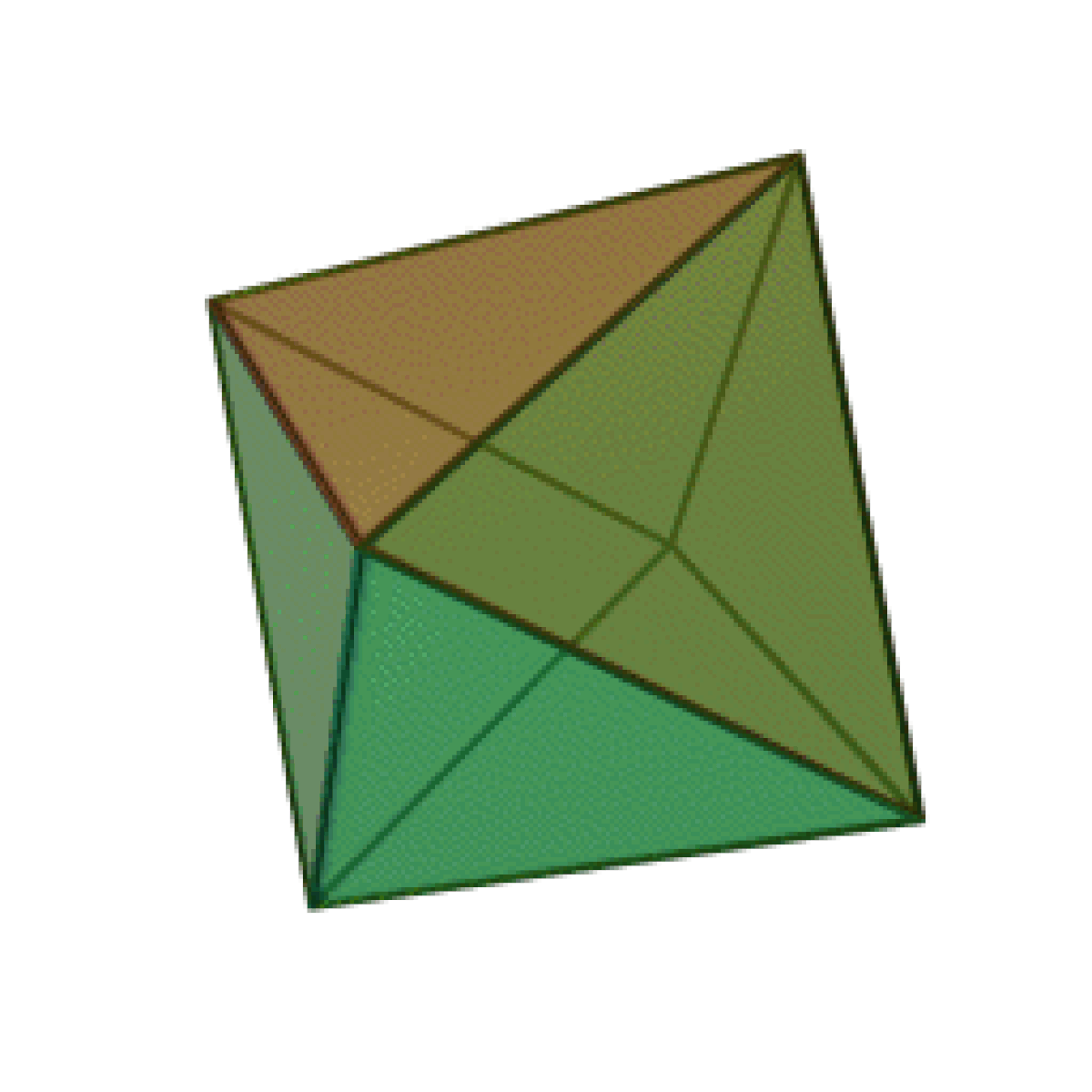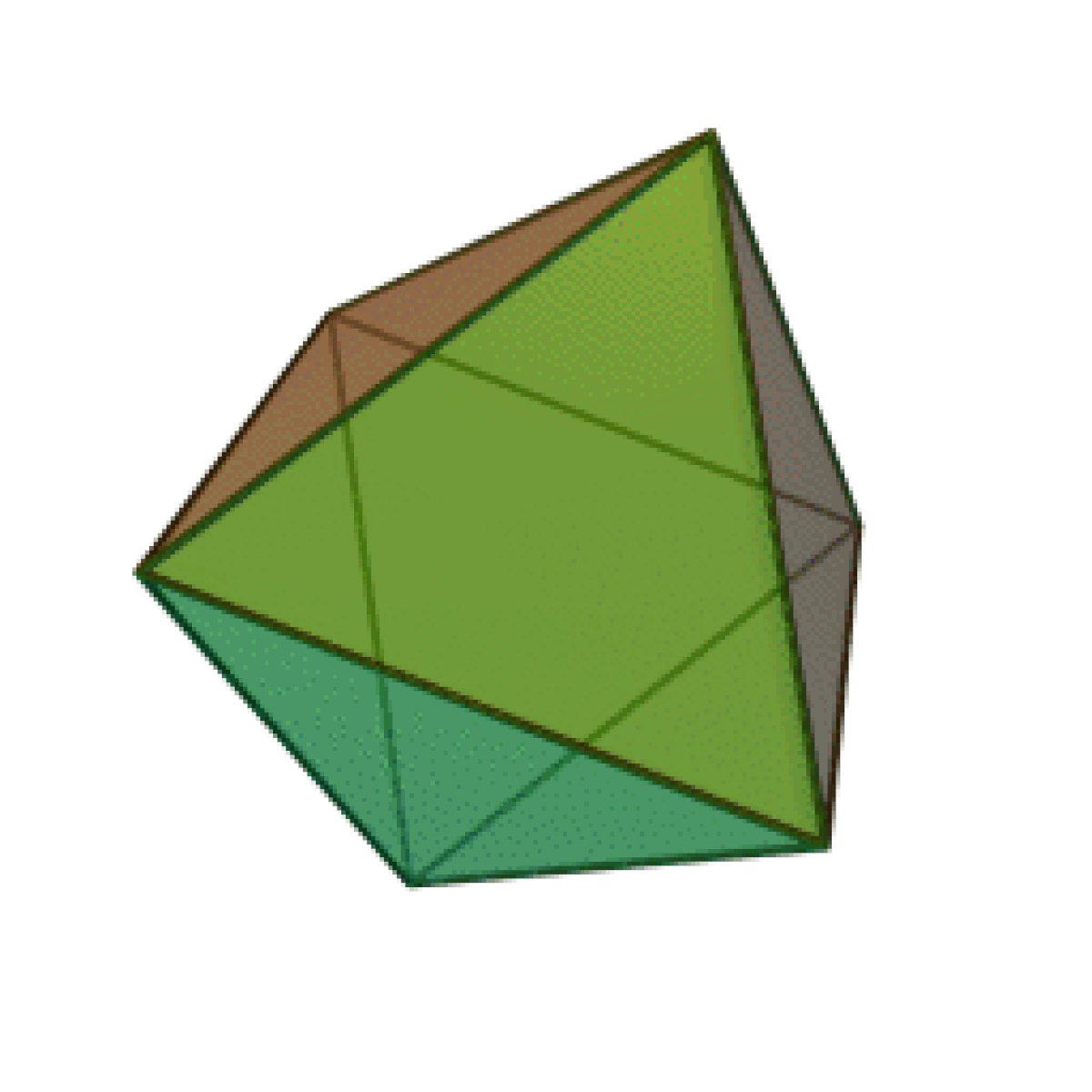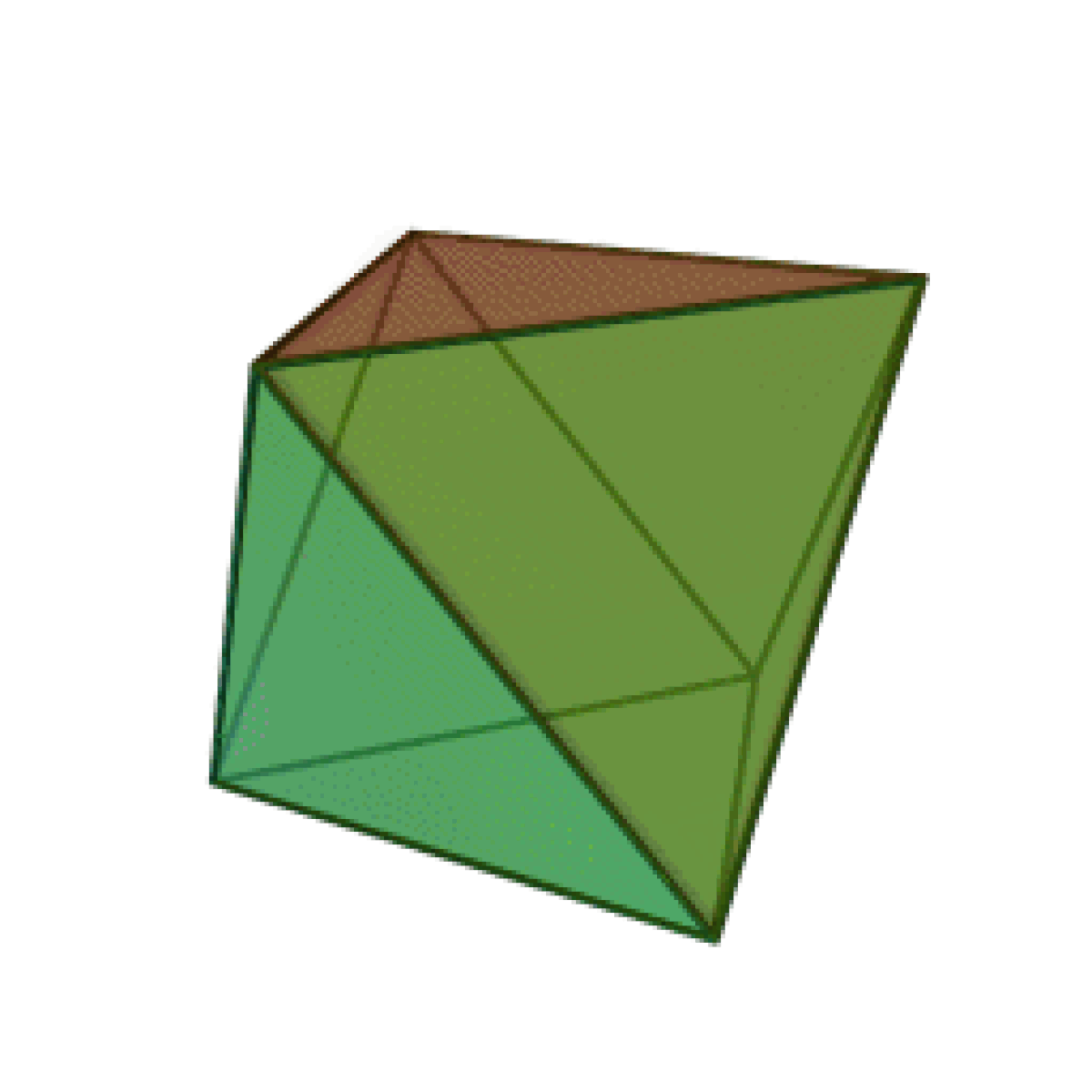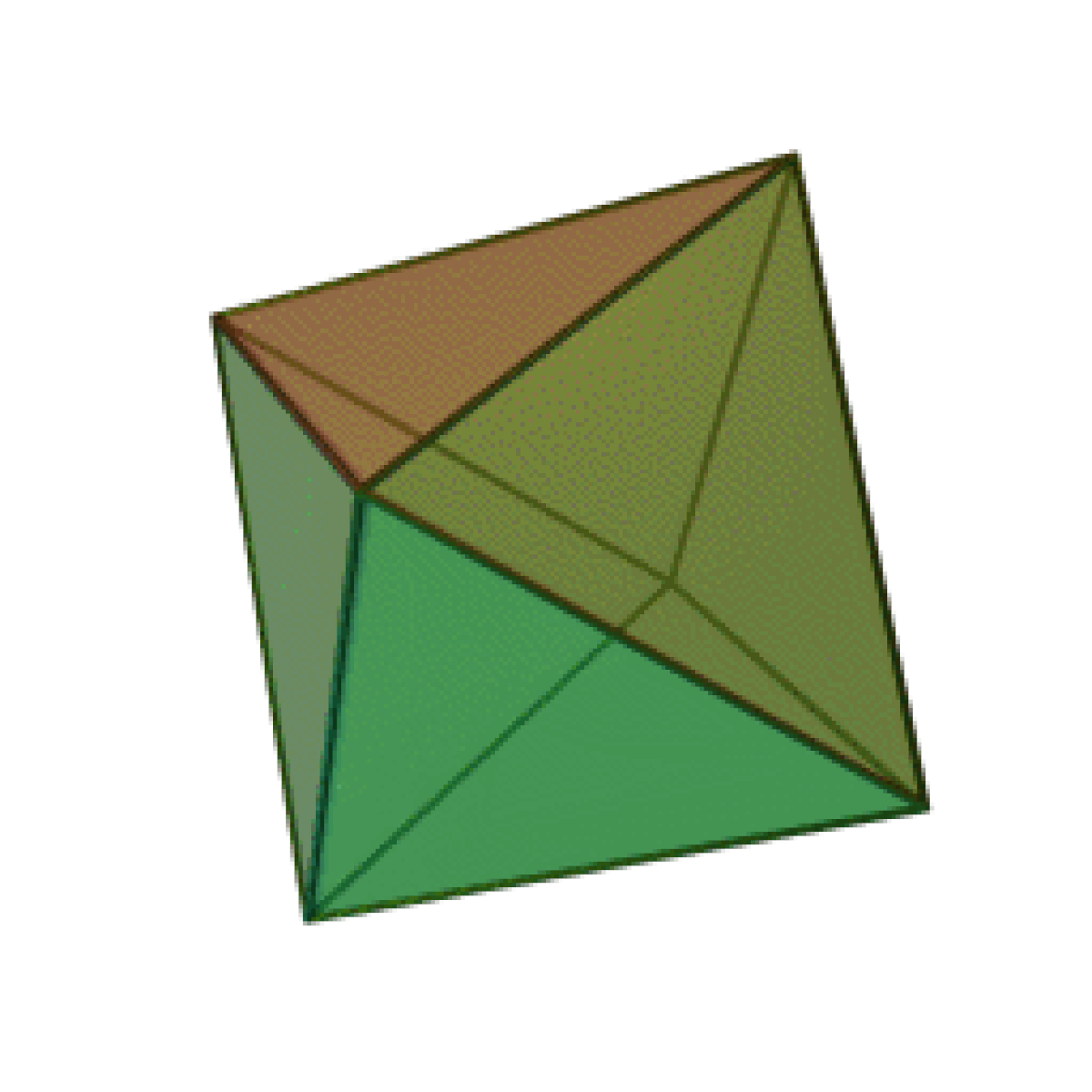 | 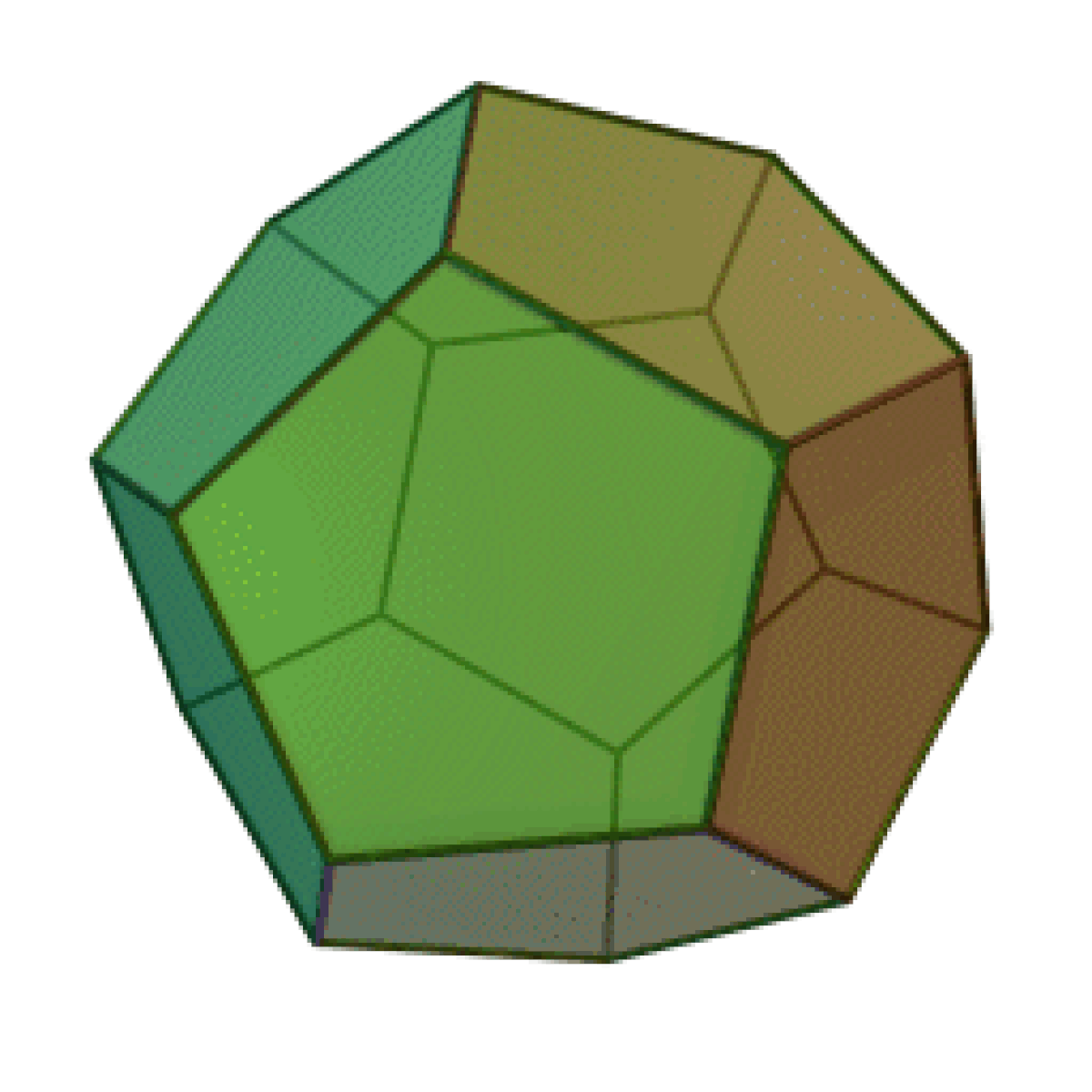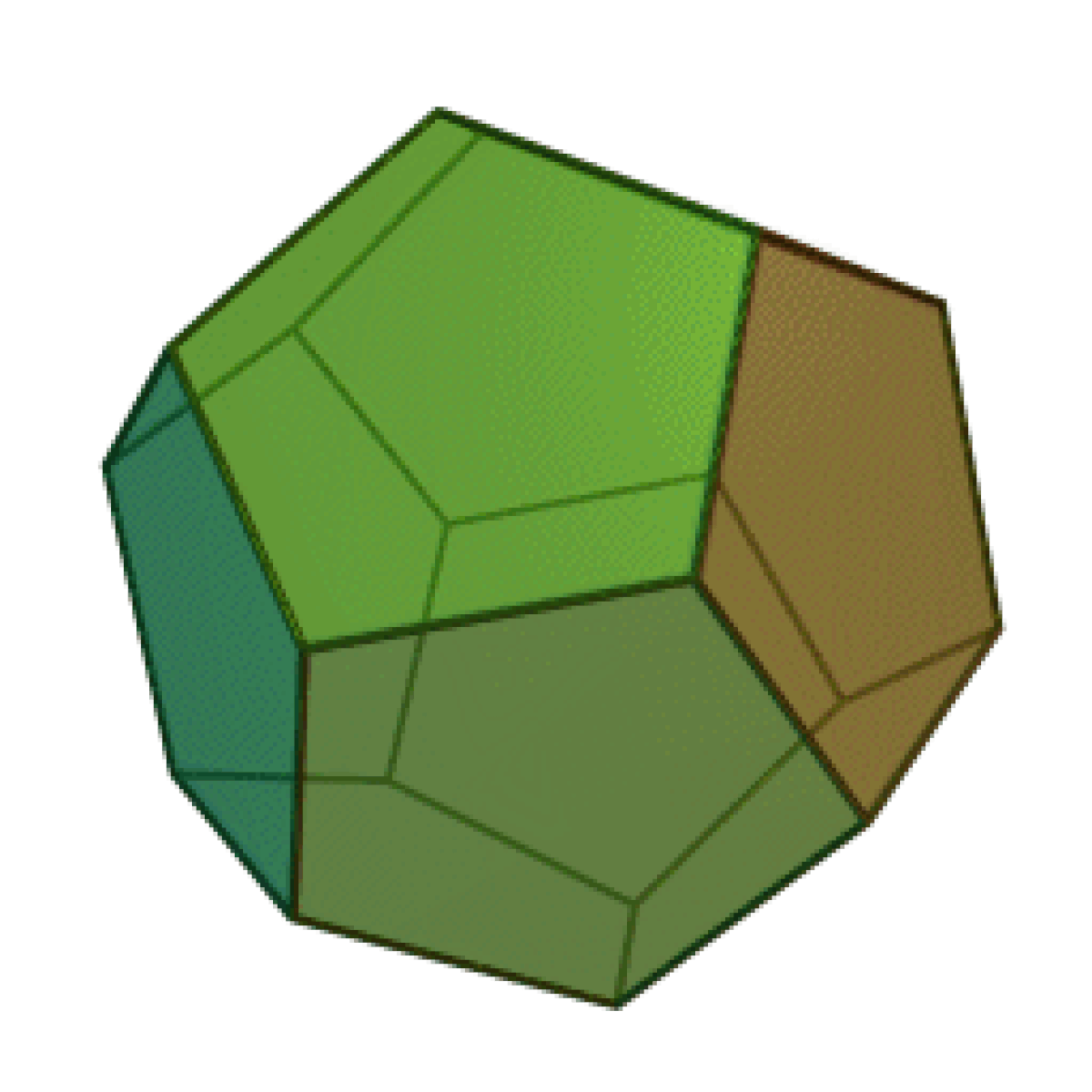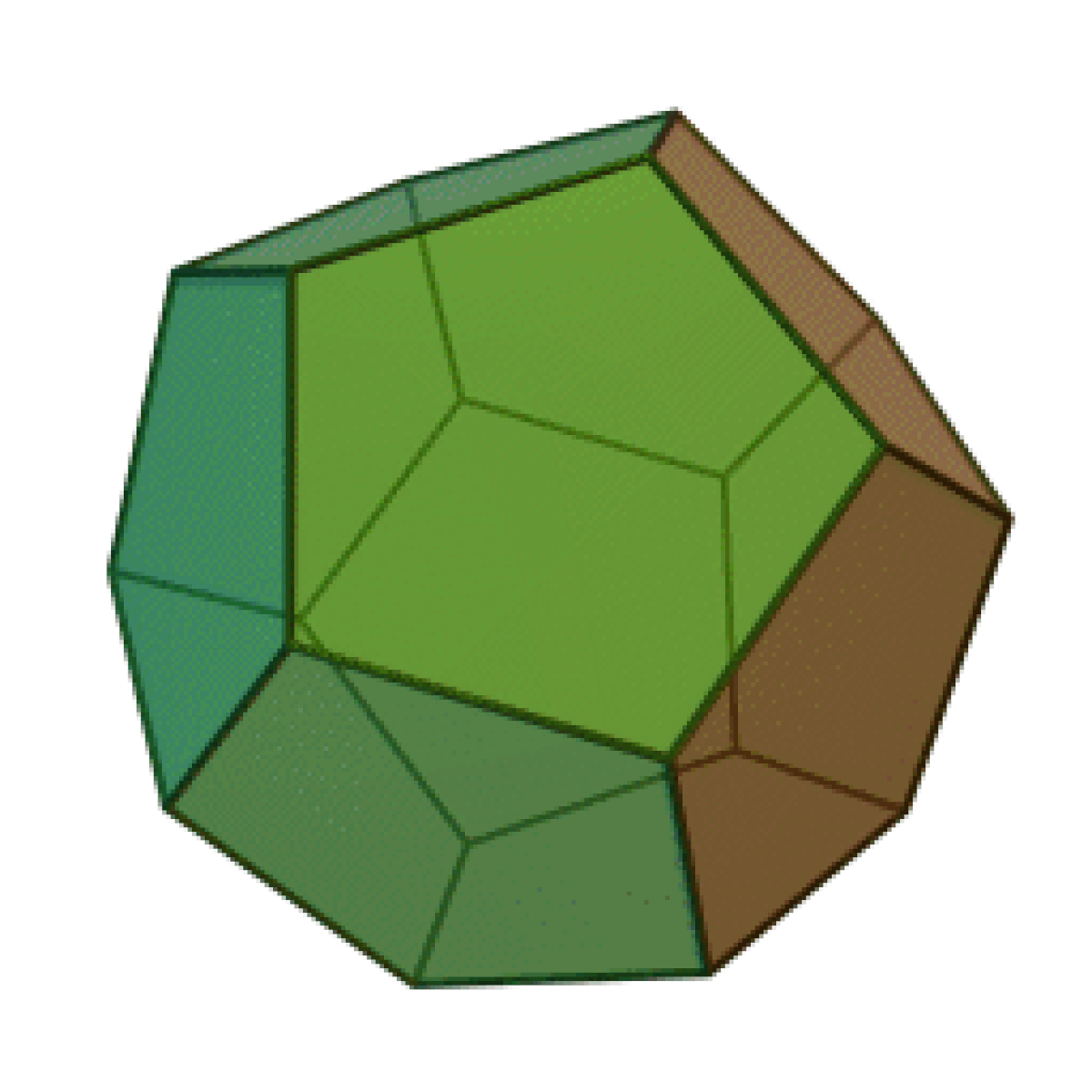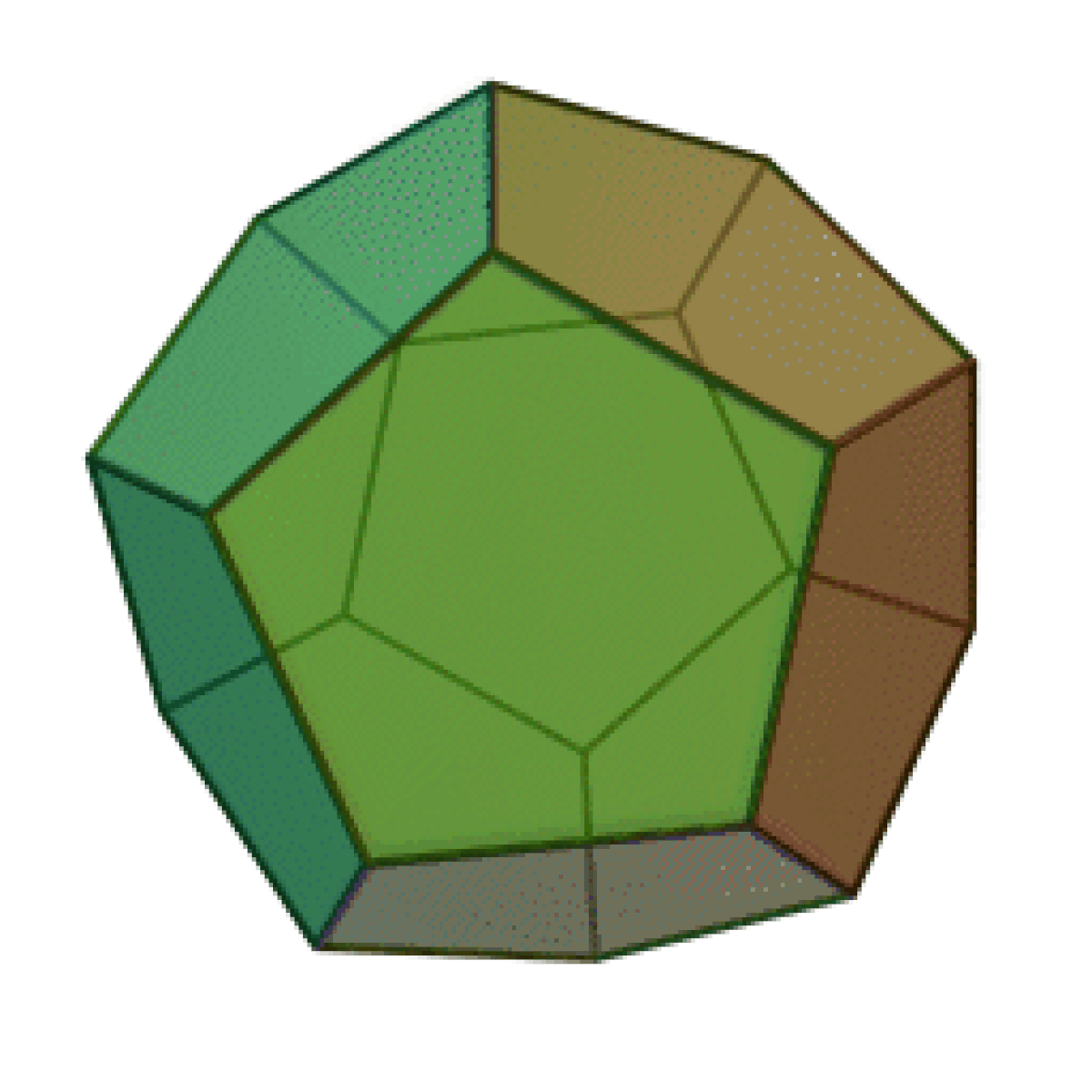 | 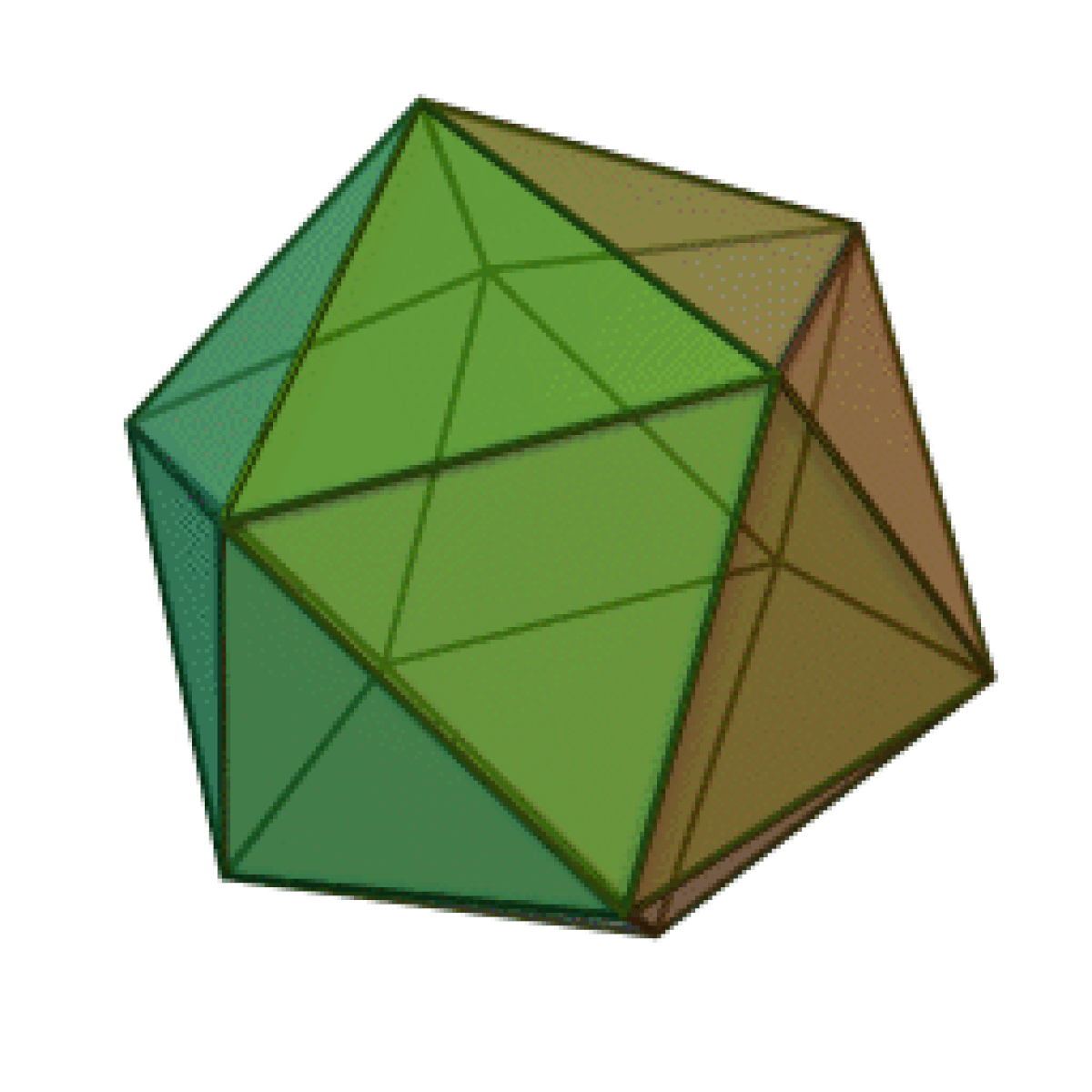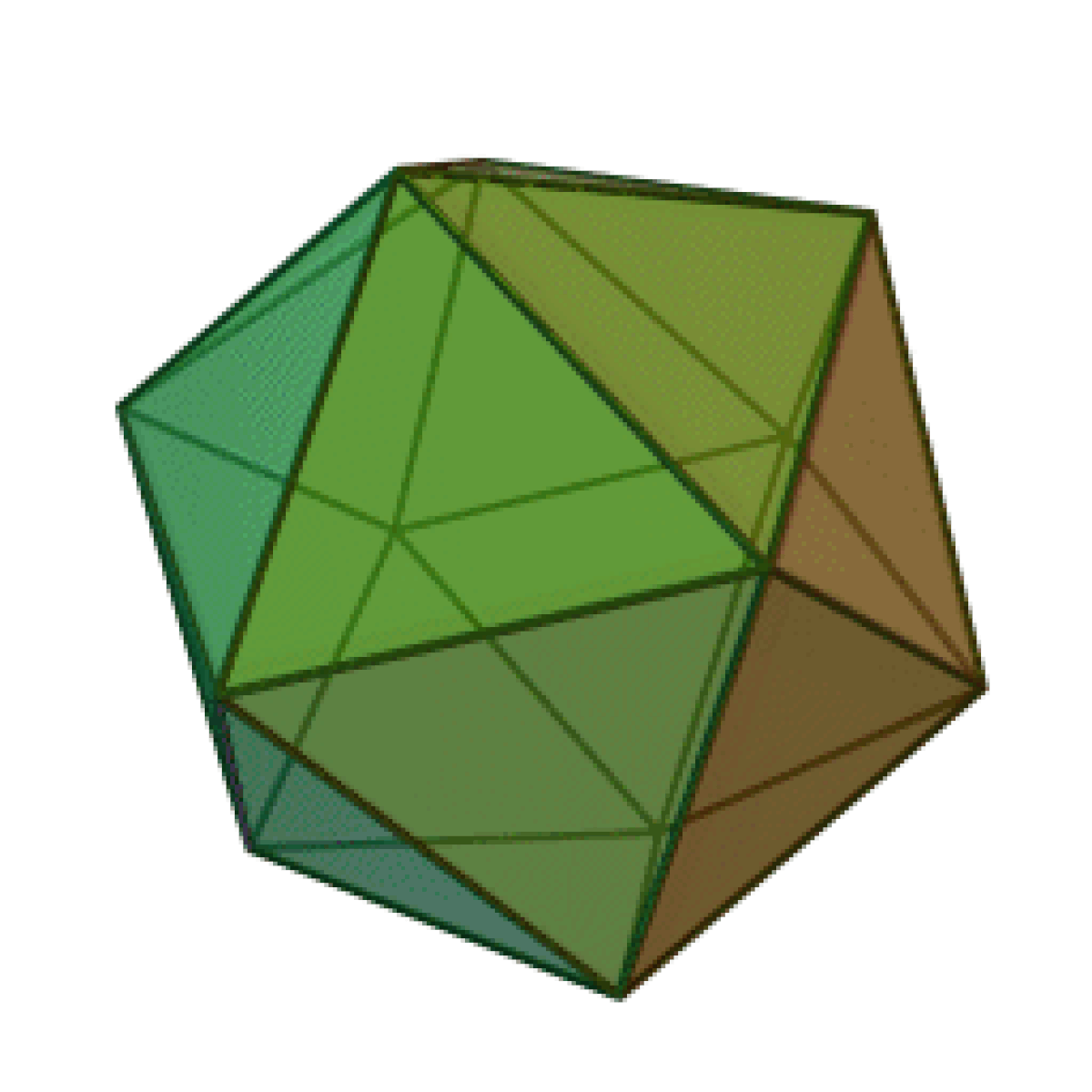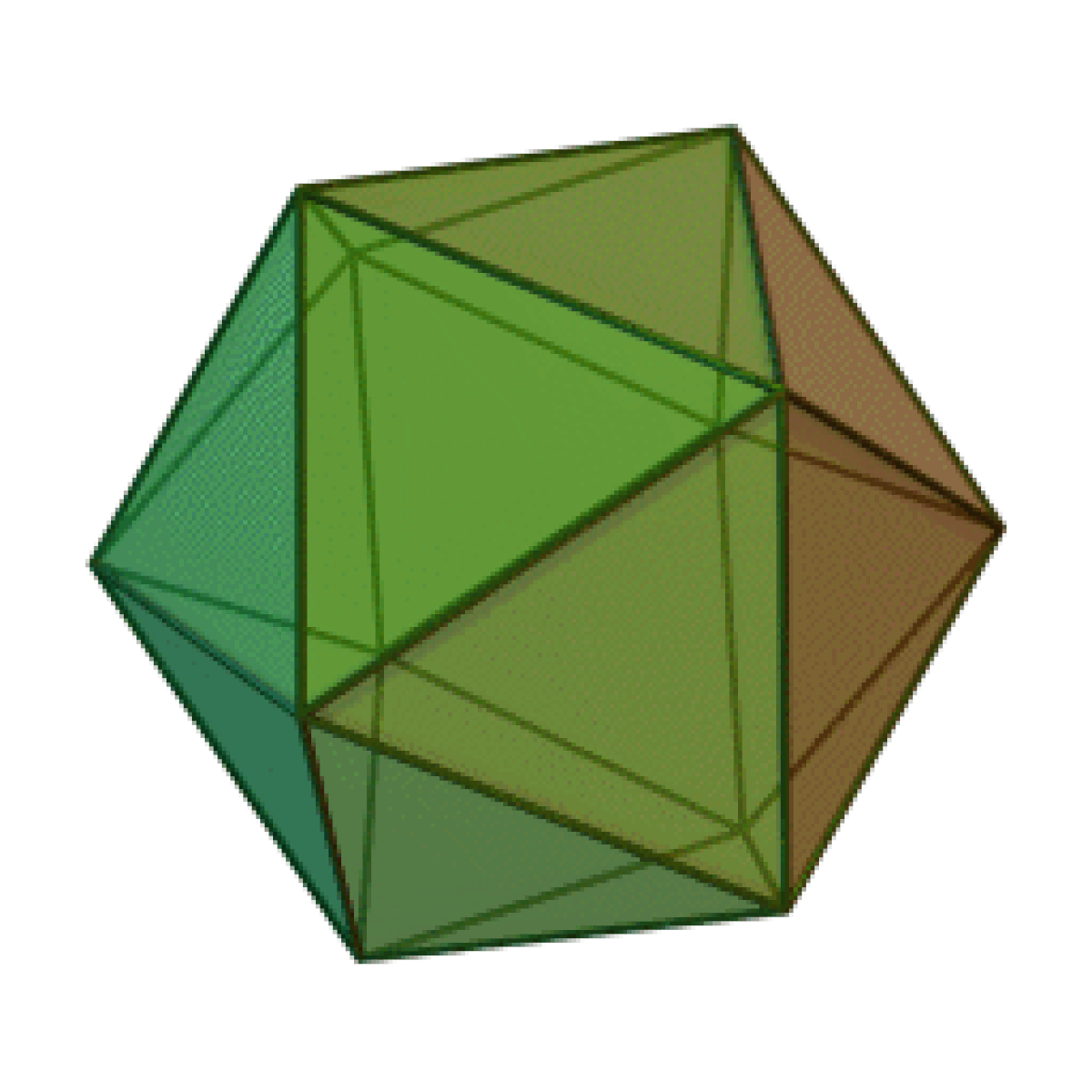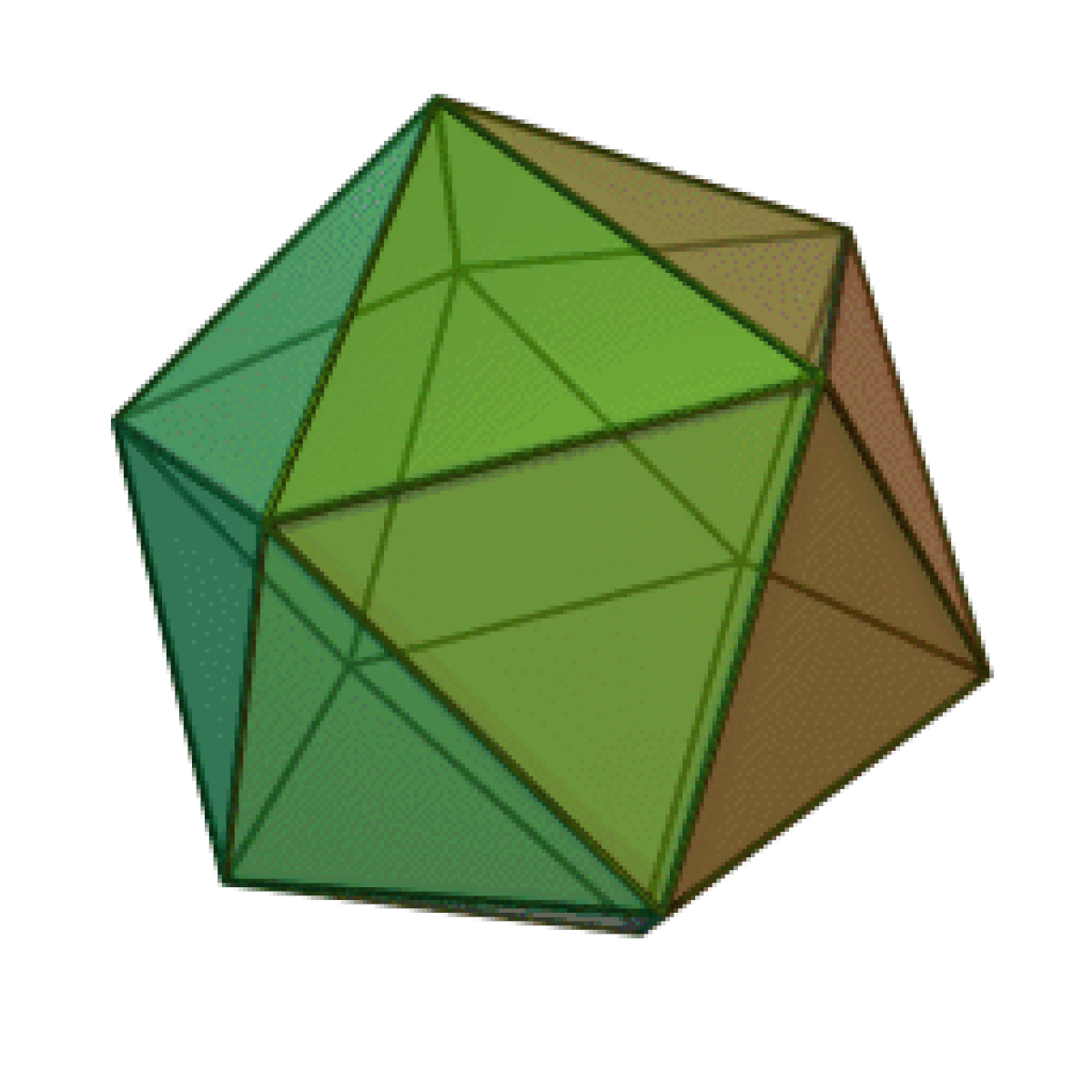 |
Le nombre de faces du solide, 4, 6, 8, 12, ou 20, est dans le préfixe du nom du solide : “tétra” pour quatre, “hexa” pour six — un cube est un hexaèdre régulier —, “octa” pour huit, “dodéca” pour douze, “icosa” pour vingt. L’adjectif “régulier” sera souvent implicite dans cette page.
Pendant des milliers d’années, les solides de Platon furent un sujet d’étude de géomètre en raison de leur esthétique et de leurs symétries. Leur nom en l’honneur du philosophe grec Platon rappelle une théorie, qui associe les Éléments physiques — les quatre éléments — à quatre solides réguliers convexes. Longtemps le nombre cinq et le nombre d'or furent des objets fétiches, associés au dodécaèdre de Platon. Il en est resté le mot “quintessence”. D’aucuns ont vu dans le nombre d’or une preuve de l’existence de Dieu. Dans ce tableau qui nous présente Luca Pacioli, auteur de La Divine Proportion (de divina proportione), un dodécaèdre de Platon est exposé en bas à droite, sans doute construit à partir d’un patron.
Histoire
Les peuples néolithiques d'Écosse ont construit des modèles en pierre des cinq solides au moins 1 000 ans avant Platon (Atiyah et Sutcliffe 2003). Ces modèles sont gardés au Ashmolean Museum à Oxford.
Dans l'histoire des mathématiques de la Grèce antique, on peut tracer la chronologie suivante. Les pythagoriciens ont eu une connaissance empirique de trois solides : le tétraèdre (la pyramide), l'hexaèdre (le cube), le dodécaèdre (douze faces). Qui exactement connaissait ? Selon Proclos, Pythagore lui-même (vers 530 av. J.-C.). Mais ce peut être son disciple Hippase de Métaponte, ou, plus vraisemblablement, Archytas de Tarente (vers 360 av. J.-C.). Peut-être Hippase a construit, le premier, le dodécaèdre. Il n'est pas fait mention de la pyramide avant Démocrite (fragment 155), actif vers 430 av. J.-C. Archytas aurait le premier construit le cube, pour résoudre le problème de la duplication du carré. Le premier, Platon mentionne le dodécaèdre, dans le Phédon (110b), qui date d'env. 383 av. J.-C. Le mathématicien Théétète d'Athènes (mort en 395 ou 360 av. J.-C.) a découvert les deux autres solides : l'octaèdre et l'icosaèdre ; surtout, il les a construits, le premier, tous les cinq. Platon a philosophé là-dessus.
Les solides de Platon jouent un rôle premier dans la philosophie de Platon, à partir duquel ils ont été nommés. Platon, dans le dialogue Timée (env. 358 av. J.-C.), associait chacun des quatre Éléments physiques (la Terre, l'Air, l'Eau et le Feu) avec un solide régulier. La Terre était associée avec le cube (Timée, 55d), l'Air avec l'octaèdre, l'Eau avec l'icosaèdre et le Feu avec le tétraèdre. Il existait une justification pour ces associations : la chaleur du Feu semble pointue et comme un poignard (comme un peu le tétraèdre). L'Air est constitué de l'octaèdre ; ses composants minuscules sont si doux qu'on peut à peine les sentir. L'Eau, l'icosaèdre, s'échappe de la main lorsqu'on la saisit comme si elle était constituée de petites boules minuscules. Par contraste, un solide fortement sphérique, l'hexaèdre (cube) représente la Terre. Ces petits solides font de la poussière lorsqu'ils sont émiettés et se cassent lorsqu'on s'en saisit, une grande différence avec l'écoulement doux de l'eau. Pour le cinquième solide de Platon, le dodécaèdre, Platon remarque obscurément, "...le dieu utilisé pour arranger les constellations sur tout le ciel ". Platon mettait en correspondance le dodécaèdre avec le Tout (Phédon, 110b ; Timée, 55c), parce que c'est le solide qui ressemble le plus à la sphère. Aristote a nommé ce cinquième élément, aithêr (aether en Latin, "éther" en Français) et a postulé que l'univers était fait de cet élément, et qu'il était substantiel à tout les autres, qu'il les contenait tous.
Speusippe, le successeur de Platon à l'Académie (en 348 av. J.-C.) a repensé la tradition pythagoricienne sur les cinq solides (Pythagore, Hippase, Archytas).
Euclide a donné une description mathématique complète des solides de Platon dans les Éléments (env. 300 av. J.-C.) ; le dernier livre (Livre XIII) qui est consacré à leurs propriétés. Les propositions 13–17 dans le Livre XIII décrit la construction du tétraèdre, de l'octaèdre, du cube, de l'icosaèdre et du dodécaèdre dans cet ordre. Pour chaque solide, Euclide trouve le rapport du diamètre à la sphère circonscrite à la longueur des arêtes. Dans la proposition 18, il argumente qu'il n'existe pas plus de polyèdres réguliers convexes. Beaucoup des informations dans le Livre XIII est probablement dérivé du travail de Théétète.
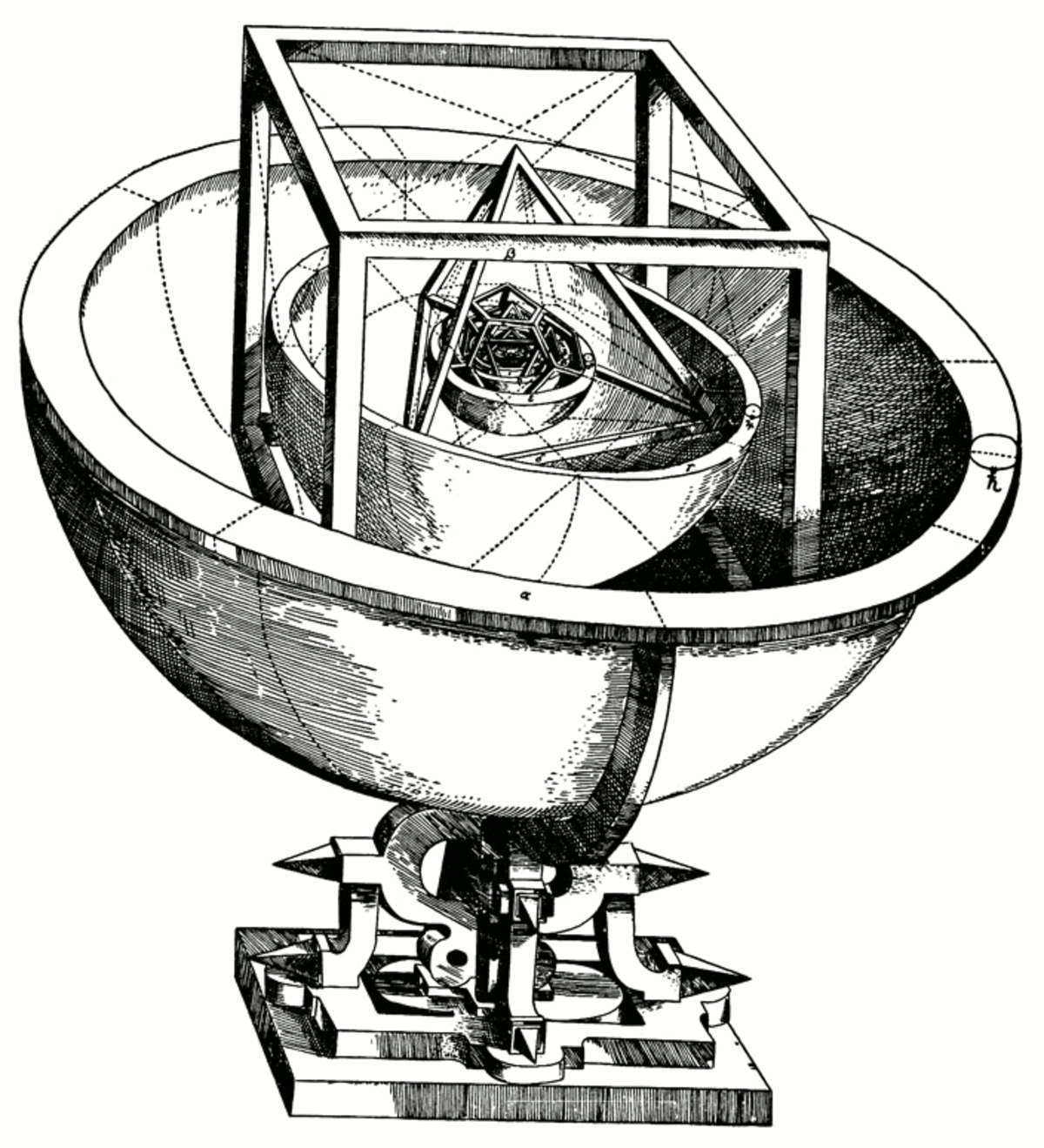
Au XVIe siècle, l'astronome allemand Johannes Kepler essaya de trouver une relation entre les cinq planètes connues à l'époque (en excluant la Terre) et les cinq solides de Platon. Dans le Mysterium Cosmographicum, publié en 1596, Kepler présenta un modèle de système solaire dans lequel les cinq solides étaient fixés les uns dans les autres et séparés par une série de sphères inscrites et circonscrites. Les six sphères correspondaient chacune aux planètes (Mercure, Vénus, la Terre, Mars, Jupiter et Saturne). Les solides étaient ordonnés de l'intérieur vers l'extérieur, le premier étant l'octaèdre, suivi de l'icosaèdre, du dodécaèdre, du tétraèdre et finalement le cube. De cette manière, la structure du système solaire et les relations de distances entre les planètes étaient dictées par les solides de Platon. Vers la fin, l'idée originale de Kepler a été abandonnée, mais de cette recherche émergèrent la découverte des solides de Kepler, la constatation que les orbites des planètes ne sont pas des cercles, et les lois du mouvement planétaire de Kepler pour lesquelles il est maintenant célèbre.


















































