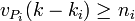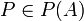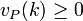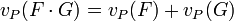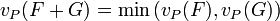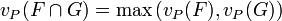Idéal fractionnaire - Définition
La liste des auteurs de cet article est disponible ici.
Définitions
Dans tout cet article, A désigne un anneau commutatif unitaire et K son anneau total des fractions : si A est intègre (ce qui sera le cas la plupart du temps), K est donc le corps des fractions de A, et dans le cas général, K est l'anneau localisé S-1A de A par rapport au sous-ensemble S des éléments réguliers (i.e. non diviseurs de zéro).
- Un sous-A-module M de K est dit inversible s'il existe un sous-A-module N tel que M.N=A, où M.N désigne le sous-module produit engendré par les produits d'éléments de M et de N.
- Un idéal fractionnaire de A est une partie de K de la forme d -1J où d est un élément régulier de A et J un idéal de A. Autrement dit, c'est un sous-A-module M de K tel qu'il existe un élément régulier d de A pour lequel d.M est inclus dans A.
- Un tel idéal fractionnaire est dit principal s'il est engendré (comme A-module) par un élément, autrement dit s'il est de la forme d -1J où J est un idéal principal de A.
Attention à cette appellation trompeuse : un idéal fractionnaire de A n'est pas toujours un idéal de A. En fait les idéaux de A sont exactement, parmi ses idéaux fractionnaires, ceux qui sont inclus dans A.
On remarque aussitôt que
- tout sous-A-module inversible de K est un idéal fractionnaire,
- l'ensemble des idéaux fractionnaires inversibles forme un groupe abélien (pour le produit défini plus haut),
- tout idéal fractionnaire inversible est de type fini en tant que A-module, autrement dit est de la forme d -1J avec J idéal de type fini. En particulier, tout idéal inversible de A est de type fini,
- si un idéal fractionnaire F est inversible alors son inverse (qu'on notera F -1) est le sous-A-module de K constitué des éléments k tels que kF soit inclus dans A. Dit autrement : F est inversible si et seulement si son produit par ce sous-module est égal à A tout entier.
Groupe des classes d'idéaux
Les idéaux fractionnaires principaux non nuls forment un sous-groupe du groupe des idéaux fractionnaires non nuls. Le groupe quotient est appelé groupe des classes. Si A est l'anneau des entiers algébriques d'un corps de nombres alors son groupe des classes est d'ordre fini. Ce résultat est une des clés permettant de résoudre des équations diophantiennes et particulièrement celle liée au dernier théorème de Fermat.
Toutes ces propriétés sont étudiées aussi, dans le cadre plus simple des entiers quadratiques, dans l'article Idéal de l'anneau des entiers d'un corps quadratique.
Valuation
On suppose ici que A est un anneau verifiant la propriété 2 du théorème précédent, et toutes ses conséquences (propriétés 3 à 5, intégrité, noethérianité, unicité de la décomposition en premiers). On va expliciter les valuations sur A qui permettent de compléter la preuve de
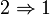
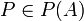
L'unicité de la décomposition en facteurs premiers des idéaux fractionnaires permet, comme pour les entiers naturels ou les rationnels, de définir une valuation sur le groupe multiplicatif Fr(A) :
-
- L'application vP qui à un idéal fractionnaire F non nul associe l'exposant de P dans sa décomposition en idéaux premiers, et qui associe à l'idéal nul la valeur infinie, est appelée valuation sur Fr (A) en P.
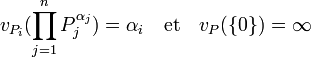
Des résultats du paragraphe précédent on déduit immédiatement que pour tous
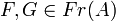
Ceci permet de définir une valuation sur K en restreignant vP aux idéaux fractionnaires principaux non nuls :
-
- l'application qui à un élément k du corps des fractions K de A associe vP(kA) est appelée valuation sur K en P. Cette application est encore notée vP.
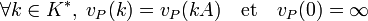
Sur K, la famille de valuations (vP), quand P parcourt maintenant l'ensemble P(A) des idéaux premiers non nuls, vérifie en outre :
-
- Pour tout élément non nul x de A, vP(x) n'est strictement positif que pour un ensemble fini d'idéaux
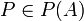
- Pour tout élément non nul x de A, vP(x) n'est strictement positif que pour un ensemble fini d'idéaux
Autrement dit, x n'appartient qu'à un nombre fini d'idéaux premiers.
-
- « Théorème d'approximation » : Soient
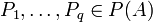
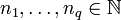
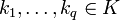
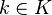
- « Théorème d'approximation » : Soient
![i\in[1,q]](https://static.techno-science.net/illustration/Definitions/autres/8/8f880293690c9a638771d7a6f70d081d_4ef7731abc48aede34cc4c536ead62f3.png)