Idéal fractionnaire - Définition
La liste des auteurs de cet article est disponible ici.
Caractérisations des anneaux de Dedekind
La définition d'un anneau de Dedekind adoptée par de nombreux auteurs, et reprise dans l'article Anneau de Dedekind est : anneau (commutatif unitaire) intègre, noethérien, intégralement clos, et dont tout idéal premier non nul est maximal. Nous la reprenons ici, mais nous verrons qu'elle équivaut à celle due à Dedekind (anneau dont tout idéal non nul est inversible), plus adaptée à l'objectif d'un analogue, en termes d'idéaux, du théorème fondamental de l'arithmétique.
Théorème — Les propriétés suivantes sont équivalentes :
- A est un anneau de Dedekind,
- tout idéal premier non nul de A est inversible,
- tout idéal non nul de A est inversible,
- A est intègre et tout idéal non nul de A est produit d'idéaux maximaux,
- A est intègre et tout idéal de A est produit d'idéaux premiers.
De plus, si A est un anneau de Dedekind, la décomposition de tout idéal non nul en produit d'idéaux premiers est unique (à l'ordre près des facteurs).
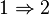
Par ailleurs, A étant noethérien, soit (p1, ... , pr) une famille finie génératrice de P. Chaque pi appartient à t.AP, donc il existe dans A un élément a n'appartenant pas à P tel que les (a/t).pi appartiennent à A, si bien que (a/t).P est inclus dans A.
Définissons l'idéal fractionnaire Q = A + (a/t)A et vérifions qu'il est inverse de P. Par construction, Q.P est un idéal de A contenant P. Puisqu'il contient aussi l'élément (a/t).t=a qui n'est pas dans P, et que P est maximal, on en déduit que Q.P = A.
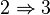
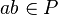
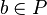
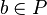
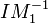
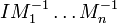
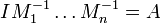
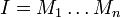
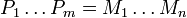
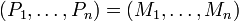
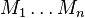
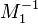
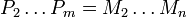
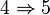
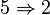
- Bourbaki, Éléments de mathématique, AC chap. 5 à 7, Springer (2006) chapitre 7 § 2 exercice 9, ou
- Oscar Zariski et Pierre Samuel, Commutative algebra, vol. 1 chap. V § 6 theorem 10, ou encore
- théorème 11.149 (attribué à Matusita) dans Aviva Szpirglas, Algèbre L3 : Cours complet avec 400 tests et exercices corrigés , ou dans son extrait, donné en lien externe
(dans ces trois sources, la série d'arguments est la même).
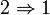
Il en résulte immédiatement que si A est un anneau de Dedekind alors
- le groupe des idéaux fractionnaires inversibles est le plus gros qu'on puisse espérer : il est constitué de l'ensemble Fr (A) de tous les idéaux fractionnaires non nuls, (car un tel idéal est de la forme d-1J = J.(dA)-1 avec J idéal de A non nul de A donc inversible)
- le groupe Fr (A) est le groupe abélien libre sur l'ensemble P(A) des idéaux premiers non nuls de A, c'est-à-dire que tout idéal fractionnaire se décompose de manière unique en un produit fini de puissances positives ou négatives d'idéaux premiers, (l'existence d'une telle décomposition pour les idéaux fractionnaires se déduit de celle pour les idéaux, et de l'écriture ci-dessus d'un idéal fractionnaire ; l'unicité également, en se ramenant, par produit, à des puissances positives),
- un idéal fractionnaire est un idéal de A si et seulement si toutes les puissances, dans sa décomposition en produit d'idéaux premiers, sont positives (« si » est immédiat, « seulement si » se déduit de la fin du théorème).

















































