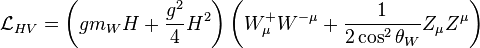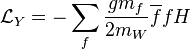Interaction électrofaible - Définition
La liste des auteurs de cet article est disponible ici.
Eléments du formalisme théorique de la théorie électrofaible
Avant la brisure de symétrie électrofaible
Comme toutes les théories des champs formelles, la théorie électrofaible est fondée sur l'étude d'un lagrangien, qui est une densité dans l'espace-temps formée par un polynôme des champs des particules impliquées dans la théorie, ainsi que de leurs dérivées.
Le lagrangien de l'interaction électrofaible est composé de quatre parties, avant la brisure de la symétrie électrofaible.
Le terme g décrit l'interaction entre les 3 particules W et la particule B.
Le terme f donne le terme cinétique des fermions du modèle standard. L'interaction entre bosons de jauge et fermions a lieu par le biais des dérivées covariantes (au sens des théories de jauge).
Le terme h décrit le champ de Higgs complexe h.
Ce terme a un signe inhabituel pour le terme quadratique correspondant usuellement à la masse. Il en résulte que la valeur h = 0 est instable. Le champ prend donc dans le vide une valeur correspondant au minimum de |h| 2 - v 2/2, soit |h| = v/4. Ceci fixe le module de la valeur de h dans le vide, mais en laisse la phase arbitraire. Le choix de la phase déterminera une orientation spécifique dans le groupe de jauge global, et en brisera donc la symétrie.
Le terme y donne l'interaction de Yukawa qui engendrera les masses de fermion quand le Higgs aura acquis une valeur moyenne dans le vide.
Après la brisure de symétrie électrofaible
Le lagrangien se réorganise quand le boson de Higgs acquiert une valeur moyenne dans le vide. En raison de sa complexité, ce lagrangien se décrit au mieux en séparant explicitement la valeur constante du champ de Higgs dans le vide, ce qui amène à le décomposer en différentes parties comme suit :
Le terme cinématique
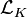
où la somme parcourt tous les fermions de la théorie (quarks et leptons), et les champs
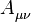
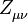
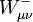
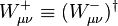
(remplacer X par le champ concerné, et f abc par les constantes de structure du groupe de jauge). Il apparaît bien que le champ A n'acquiert pas de masse, tandis que Z, W ± en acquièrent une, qui est élevée.
Les composantes des courants neutre
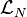
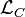
-
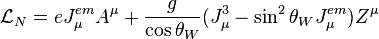
où le courant électromagnétique
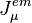
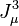
-
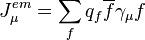
et :
q f et I f 3 sont les charges électrique et isospin faible des fermions.
L'interaction par l'intermédiaire des courants neutres se décompose donc en une interaction propagée par le champ A de masse nulle, et en une interaction propagée par le champ Z, qui ne peut être à l'état virtuel que sur une distance infime proportionnelle à 1/mZ.
La partie courant chargé du lagrangien est :
L'interaction propagée par le champ W est également ponctuelle à basse énergie. C'est l'interaction ponctuelle de Fermi.
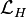
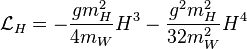
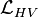
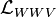
![\mathcal{L}_{WWV}=-ig[(W_{\mu\nu}^+W^{-\mu}-W^{+\mu}W_{\mu\nu}^-)(A^\nu\sin\theta_W-Z^\nu\cos\theta_W)+W_\nu^-W_\mu^+(A^{\mu\nu}\sin\theta_W-Z^{\mu\nu}\cos\theta_W)]](https://static.techno-science.net/illustration/Definitions/autres/1/17e507ca8a9a9c019d3b9f5ccc8ec1a8_b5f71c4f45c02e4978ce930300c50103.png)
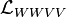
![\mathcal{L}_{WWVV} = -\frac{g^2}4 \left\{[2W_\mu^+W^{-\mu} + (A_\mu\sin\theta_W - Z_\mu\cos\theta_W)^2]^2 - [W_\mu^+W_\nu^- + W_\nu^+W_\mu^- + (A_\mu\sin\theta_W - Z_\mu\cos\theta_W) (A_\nu\sin\theta_W - Z_\nu\cos\theta_W)]^2\right\}](https://static.techno-science.net/illustration/Definitions/autres/9/95b992dfdd5c0b364636996f62688067_6d5713f7f2341f9135b1a2d32639972e.png)
Les 4 interactions précédentes ne sont encore pas sujettes à l'expérience, compte tenu du fait que l'on n'a même pas encore observé le boson de Higgs, et l'interaction de bosons W ± ou Z 0 réels entre eux est peut-être plus difficile encore à observer.
et finalement
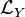
Cette dernière interaction, ou celle entre des bosons vecteurs lourds virtuels, permettrait de produire et d'observer des bosons de Higgs, peut-être auprès du LHC.
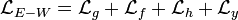
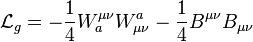
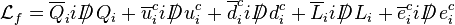
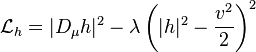
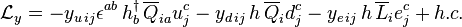
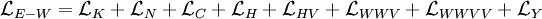
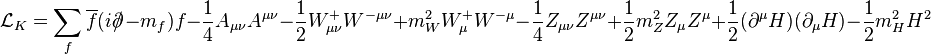
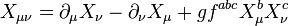
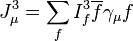
![\mathcal{L}_C=-\frac g{\sqrt2}\left[\overline u_i\gamma^\mu\frac{1-\gamma^5}2M^{CKM}_{ij}d_j+\overline\nu_i\gamma^\mu\frac{1-\gamma^5}2e_i\right]W_\mu^++h.c.](https://static.techno-science.net/illustration/Definitions/autres/7/7e50221ac5f6c3c7de5c6ef69f07c056_476481bf8ed659baccf1d63264b4358e.png)