Jean-Robert Argand - Définition

Introduction

Jean-Robert Argand, né le 18 juillet 1768 à Genève et mort le 13 août 1822 à Paris, est un mathématicien suisse.

En 1806, alors qu'il tient une librairie à Paris, il publie une interprétation géométrique des nombres complexes comme points dans le plan, en faisant correspondre au nombre (où i est la racine carrée de -1) le point de coordonnées (a,b). Pour cette raison, le plan, vu comme ensemble des nombres complexes, est parfois appelé le plan d'Argand.

Les complexes selon Argand

Produit par proportion géométrique

Dans son traité Essai sur une manière de représenter les quantités imaginaires par des constructions géométriques , Argand commence par associer à chaque nombre positif a une ligne , horizontale orientée vers la droite et de longueur a. Puis, il remarque qu'il peut associer à chaque nombre négatif -b, une ligne horizontale orientée vers la gauche de longueur b. La somme consiste à la mise bout à bout de lignes. Les opérations du produit et de la racine carré consiste à travailler sur les proportionnalités :

(a ; b) est proportionnel à (c ; d) si les rapports a : b et c : d sont identiques (même valeur absolue et même signe)

Le produit de a par b devient donc le nombre ab tel que (1;a ) et (b; ab) soient proportionnels. La construction géométrique d'une quatrième proportionnelle est une construction connue depuis longtemps . Donc, Argand sait construire la ligne :

Racine carrée par proportion géométrique

La racine carré de x (positif) est le nombre y (positif) tel que (1 ; y) et (y ; x) soient proportionnels. Cette construction est aussi réalisable (voir nombre constructible). Si est associé à 1, associé à y et associé à x, on dira que :

est à ce que est à .

On obtient :

ou encore :

Plan d'Argand

Le problème qui se pose ensuite est de construire la racine carrée de -1. Si est le nombre associé à -1, il s'agit de trouver une ligne telle que

soit à ce que est à .

Ceci ne peut pas se réaliser en restant sur la droite. Argand quitte donc la droite et dit que

est à ce que est à

lorsque les rapports des longueurs sont égaux et les angles AKB et BKC sont égaux .

Ce qui place le point B à la verticale du point K à une distance de 1. La ligne représente alors l'imaginaire i (noté à l'époque .)

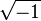
Il crée alors sur l'ensemble des "lignes dirigées" une addition (qui s'apparente à ce qu'on appelle aujourd'hui la relation de Chasles) et un produit

Produit de deux complexes

Le produit :

est la ligne telle que soit à ce que est à .

Avec la définition de proportionnalité qu'il donne dans le plan, cela signifie que

• 
• les angles NKP et AKM sont égaux.

Il démontre alors qu'un produit de lignes dirigées correspond au produit des longueurs et à la somme des angles.

Il associe alors à chaque complexe, une ligne dirigée, et montre la correspondance entre les opérations. Chaque ligne dirigée a donc deux représentations possibles

• par ses coordonnées cartésiennes (a ; b) qui renvoient au complexe a + ib
• par ses coordonnées polaires : longueur de la ligne et direction (ou angle) de la ligne.

Si le complexe est a + ib, la longueur de la ligne est , longueur qu'Argand appelle le module du complexe car c'est l'unité par lequel il faut le diviser pour retrouver sa direction.

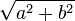
En proposant cette représentation des complexes sous forme géométrique, l'objectif d'Argand est double

1. prouver la réalité des complexes que les gens de l'époque considèrent encore comme imaginaires et comme simple artifice de calcul
2. donner un outil géométrique qui peut simplifier grandement la résolution des problèmes algébriques.

Il propose même une démonstration du théorème fondamental de l'algèbre (partiellement fausse) grâce à cet outil.