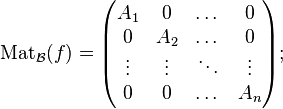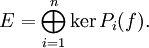Lemme des noyaux - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, le lemme des noyaux est un résultat sur la réduction des endomorphismes. Dans un espace vectoriel E sur un corps K, si un opérateur u de E est annulé par un polynôme P(X) à coefficients dans K, alors ce lemme prévoit une décomposition de E comme somme directe de sous-espaces vectoriels stables par u. Ces derniers se définissent comme noyaux de polynômes en u, les projecteurs associés étant eux-mêmes des polynômes en u.
La démonstration traduit l'identité de Bezout portant sur les polynômes à des sous-espaces vectoriels. Résultat fondamental, le lemme des noyaux conduit à la décomposition de Dunford puis à la décomposition de Jordan. Plus modestement, le lemme des noyaux montre qu'un opérateur u est diagonalisable s'il est annulé par un polynôme à racines simples.
Enoncé
Lemme des noyaux — Soit E un espace vectoriel sur un corps K et soit f un endomorphisme de E. Si
![P_1,\ldots,P_n \in K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/192527f1c86d44ab5e67ee58757eb75c_1a01e9fe9051048d3849600cdab613b5.png)
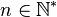
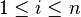
De plus, la projection sur Vi parallèlement à

Démonstration
Par récurrence sur n. On pose
Initialisation
On suppose n = 2. On a alors P = P1P2. D'après le théorème de Bézout, il existe
![(U_1,U_2) \in (K[X])^2](https://static.techno-science.net/illustration/Definitions/autres/8/8146e0bab86c36289ba6736b00e7c5cc_d9248bd983082a1a9741f43120adddd5.png)
Soit


Soit

ce qui montre que
 \in \ker P_2(f)](https://static.techno-science.net/illustration/Definitions/autres/d/d6db253332dc2cb528d8891fe30193c0_ef4d8156d9ab5979aefba7b7d8b17a02.png)
 \in \ker P_1(f)](https://static.techno-science.net/illustration/Definitions/autres/b/be11d9e6555d228ef629bd849f55068b_2e2f270acbf1750a94997642ef07f648.png)
On en déduit donc que
Hérédité
Supposons le lemme des noyaux démontré pour un


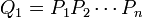

ce qui montre que le lemme des noyaux est vrai pour n + 1.
Applications
Le lemme des noyaux sert pour la réduction des endomorphismes. Par exemple :
Réduction à une forme diagonale par blocs — Soit E un espace vectoriel de dimension finie sur un corps K et soit f un endomorphisme de E. Soit
![P\in K[X]](https://static.techno-science.net/illustration/Definitions/autres/4/4facb36da11821b818abd66b424a6a76_900de20a38c2e3338cc40e60fd9ffc55.png)
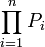
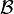

où ni = dimkerPi(f).
Par hypothèse kerP(f) = E, donc, d'après le lemme des noyaux :
Chaque sous-espace kerPi(f) est stable par f, donc la matrice de f dans n'importe quelle base de E adaptée à la décomposition précédente en sous-espaces stables, est diagonale par blocs comme souhaité.
![\bigoplus_{i=1}^n \ker \left[ P_i(f) \right] = \ker \left[ \left( \prod_{i=1}^n P_i \right)(f) \right].](https://static.techno-science.net/illustration/Definitions/autres/b/ba40b11861f53424230392d973cac669_0f9118aa760068696d0c45c421a7b969.png)
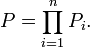
\}=[(U_1P_1P_2)(f)](x)=[U_1(f) \circ P(f)](x)=0;](https://static.techno-science.net/illustration/Definitions/autres/0/0c02733ddfe05b757fce27990462f96a_87d39726c5f2f97cd63bcea2812d76d8.png)

![\ker P(f)=\ker Q_1(f) \oplus \ker Q_2(f)= [\ker P_1(f) \oplus \cdots \oplus \ker P_n(f)]\oplus \ker P_{n+1}(f)=\bigoplus_{i=1}^{n+1} \ker P_i(f);](https://static.techno-science.net/illustration/Definitions/autres/6/603a1ad3a1e9863aa2f0cb76f3d9fd6e_13d2a572a1a7def9054bc38ce525bb8b.png)