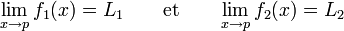Limite (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Limite d'une fonction en un point
Supposons que f : U → R soit une fonction, où U est un sous-ensemble de l'ensemble des réels. Si p est un réel, et si f est définie au voisinage de p, on dit que f admet une limite (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que |x - p| < δ, on ait |f(x) - L| < ε.
On démontre que le réel L de la définition, lorsqu'il existe, est unique et on l'appelle limite de f au point p. On le note :
-
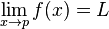
On peut démontrer que ceci est équivalent à
- pour tout suite convergente (xn) dans U de limite égale à p, la suite (f(xn)) est convergente de limite L.
Remarquons qu'une fonction peut admettre une limite en p sans être définie en p. Mais si une fonction f est définie en p et admet une limite en ce point, alors cette limite ne peut être que f(p). On dit dans ce cas que f est continue en p.
Définissons maintenant la limite épointée (ou limite par valeurs différentes) :
On dit que f admet une limite épointée (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que 0 < |x - p| < δ, on ait |f(x) - L| < ε.
De même ce nombre L est alors unique et on note :
-
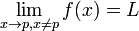
Occasionnellement, il peut être utile de n'approcher le point p que d'un seul côté.
On dit que f admet une limite à droite (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que 0 < x - p < δ, on ait |f(x) - L| < ε.
Ce nombre L est alors unique et on le note :
-
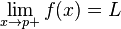
Les limites à gauche s'obtiennent en remplaçant x - p dans la dernière définition par p - x.
Il est possible aussi de considérer des limites où p ou L sont égaux à plus l'infini (+∞) ou moins l'infini (-∞).
On dit que f(x) tend vers +∞ quand x tend vers p (ou que f a pour limite +∞ en p) si
- pour tout réel R > 0, il existe un réel δ > 0 tel que pour tout x tel que |x - p| < δ on ait f(x) > R.
On dit que f(x) tend vers L quand x tend vers +∞ (ou que f a pour limite L en +∞) si
- pour tout réel ε > 0 il existe un réel S > 0 tel que pour tout x > S, on ait |f(x) - L| < ε.
Enfin, on dit que f(x) tend vers +∞ quand x tend vers +∞ (ou que f a pour limite +∞ en +∞) si
- pour tout réel R > 0 il existe un réel S > 0 tel que pour tout x tel que x > S, on ait f(x) > R.
Les définitions pour moins l'infini sont analogues.
En remplaçant ε par S comme précédemment, on peut aussi définir les limites infinies d'un seul côté (à droite ou à gauche).
Exemples
- La limite de
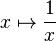
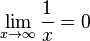
- La limite de
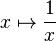
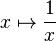

- La limite de
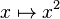
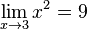
- La limite de
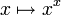
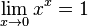
- La limite de
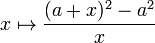
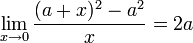
- La limite à droite de
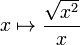
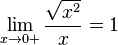
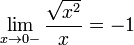
- La limite de
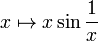
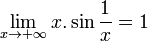
- La limite de
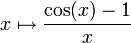
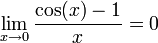
Propriétés
La limite pointée de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales.
Si p est un point de U, alors la limite de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales à f(p), si et seulement si la limite pointée de f(x) quand x tend vers p existe et est égale à f(p) et si et seulement si f est continue en p.
Si p n'appartient pas U alors la limite de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales.
Le passage à la limite des fonctions est compatible avec les opérations algébriques :
Si
alors
-
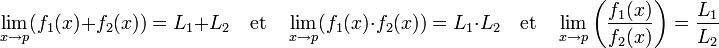
(La dernière propriété suppose que f2 ne s'annule pas dans un voisinage de p et que L2 n'est pas nul).
Ces propriétés sont aussi valables pour les limites à droite et à gauche, pour le cas p = ±∞, et aussi pour les limites infinies en utilisant les règles suivantes :
- q + ∞ = ∞ pour q ≠ -∞
- q × ∞ = ∞ si q > 0
- q × ∞ = -∞ si q < 0
- q / ∞ = 0 si q ≠ ± ∞
(voir la droite réelle achevée).
Remarquons qu'il n'y a pas de règle générale pour le cas q / 0 : cela dépend de la façon dont on s'approche de 0. Certains cas, comme par exemple 0/0, 0×∞ ∞-∞ ou ∞/∞, ne sont pas non plus couverts par ces règles.
Indétermination
Il existe certaines formes de limite où il est n'est pas possible de conclure directement en utilisant des opérations sur les limites, ce sont les formes dites indéterminées.
Indétermination de la forme 0/0 quand le résultat obtenu donne 0/0
Indétermination de la forme ∞/∞ quand le résultat obtenu donne ∞/∞
Indétermination de la forme ∞ - ∞ quand le résultat obtenu donne ∞ - ∞
Indétermination de la forme 0 × ∞ qui se ramène aux deux premiers cas en remarquant qu'une multiplication par 0 équivaut à une division par l'infini, ou qu'une multiplication par l'infini équivaut à une division par 0
Indétermination de la forme 00 qui se ramène au cas précédent en remarquant que ab peut s'écrire eb×ln(a) et que la limite de b×ln(a) est alors de la forme 0 × ∞
La règle de L'Hôpital permet souvent de lever ces indéterminations.