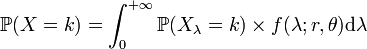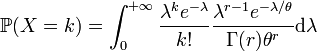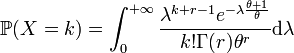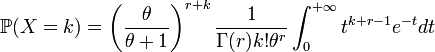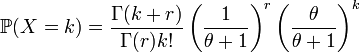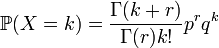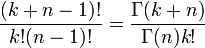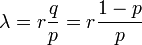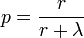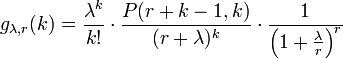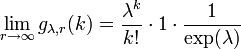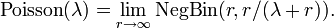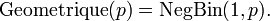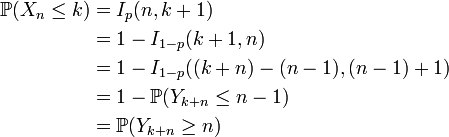Loi binomiale négative - Définition

Applications

Temps d'attente dans un processus de Bernoulli

Pour tout n entier, la loi binomiale négative est la distribution de succès et d'échecs dans une série d'épreuves de Bernouilli iid. Pour k+n épreuves de Bernoulli, avec probabilité de succès p, la loi binomiale négative donne la probabilité de k échecs et n succès, le dernier tirage étant un succès. Autrement dit, la loi binomiale négative est la distribution du nombre d'échecs avant le n ème succès dans des épreuves de Bernouilli, de probabilité de succès p.

Considérons l'exemple suivant. On lance plusieurs fois un dé honnête, et la face "1" est considérée comme un succès. La probabilité de succès à chaque épreuve est 1/6. Le nombre d'épreuves nécessaires pour obtenir 3 succès appartient à l'ensemble infini { 3, 4, 5, 6, ... }. Ce nombre d'épreuves est une variable aléatoire distribuée selon une loi binomiale négative (décalée, car l'ensemble commence à 3 et pas à 0). Le nombre d'échecs avant le troisième succès appartient à l'ensemble { 0, 1, 2, 3, ... }. Ce nombre d'échecs est aussi distribuée selon une loi binomiale négative.

Loi de Poisson «sur-dispersée»

La loi binomiale négative, en particulier dans sa paramétrisation alternative décrite plus haut, est une alternative intéressante à la loi de Poisson. Elle est particulièrement utile pour des données discrètes, à valeurs dans un ensemble positif non-borné, dont la variance empirique excède la moyenne empirique. Si une Poisson est utilisée pour modéliser de telles données, la moyenne et la variance doivent être égales. Dans ce cas, les observations sont «sur-dispersée» par rapport au modèle Poisson. Puisque la loi binomiale négative possède un paramètre supplémentaire, il peut être utilisé pour ajuster la variance indépendamment de la moyenne.

Propriétés

Mélange de Gamma-Poisson

Il arrive que l'occurrence de certains phénomènes suive une loi de Poisson de paramètre λ variant lui-même de manière aléatoire. C'est le cas lorsque le phénomène peut se produire dans des populations différentes dans lesquelles la loi de Poisson change de paramètre. C'est ce qu'on appelle des mélanges de loi de Poisson. Lorsque le paramètre λ suit une distribution Gamma de paramètres r et θ, l'occurrence du phénomène suit une loi de mélange Gamma-Poisson. La probabilité que le phénomène se réalise k fois est alors

où X_λ suit une loi de Poisson de paramètre λ et f(λ;r,θ) est la densité de la loi Gamma de paramètres r et θ (réels positifs).

Si Γ(r) est la valeur de la fonction gamma en r, on obtient alors :

Le changement de variable conduit à :

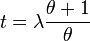
En posant et , on remarque que p + q = 1 et

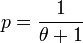
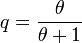
Cette formule est une généralisation de la loi précédente pour un paramètre r réel strictement positif. En effet, pour tout entier naturel n non nul,

On généralise ainsi la loi binomiale négative à un premier paramètre r réel positif. Les formules de la moyenne, de la variance et de la fonction de répartition (sous la forme I_p(r,k + 1)) restent valables.

Le mélange Gamma-Poisson de paramètres r et θ est donc une loi binomiale négative de paramètres r et .

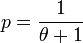
Cas limite

Si l'on note λ l'espérance de cette loi, on a les relations suivantes :

la loi de probabilité devient:

où λ est un réel positif , r un entier naturel non nul et P( r + k - 1,k), noté aussi , est le nombre de permutations ou d'arrangement de k éléments parmi r + k - 1

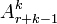
Sous cette paramétrisation, on a

qui est la loi de probabilité d'une loi de Poisson avec un paramètre λ. En d'autres termes, cette loi binomiale négative converge vers une loi de Poisson, et r régit la déviation vis-à-vis de la Poisson. La loi binomiale négative peut donc être vue comme une alternative robuste à la loi de Poisson, approchant cette loi pour r grand, mais avec une variance plus grande pour r petit.

En d'autres termes, la loi binomiale négative converge en distribution vers une Loi de Poisson, dans le sens:

Loi géométrique associée

Comme il existe deux définitions de la loi binomiale négative, il existe deux définitions de la loi géométrique. Si celle-ci modélise le nombre d'échecs avant le premier succès, elle correspond à la loi binomiale négative de paramètres 1 et p.

Si X_n est une variable aléatoire distribuée selon la loi binomiale négative de paramètres n et p, alors X_n est la somme de n variables aléatoires indépendantes distribuées selon une loi géométrique de paramètre p. Le Théorème de la limite centrale indique de plus que X_n est approximativement normal, pour n suffisamment grand.

Lien avec la loi binomiale

En outre, si Y_k+n est une variable aléatoire distribuée selon une loi binomiale de paramètre k + n et p, alors

La dernière ligne s'interprète ainsi: c'est la probabilité qu'après k+n épreuves, il y ait au moins n succès. Ainsi, la loi binomiale négative peut être vue comme l'inverse de la loi binomiale.

Somme

La somme de deux variables aléatoires indépendantes et identiquement distribuées selon une loi binomiale négative de paramètres p et respectivement r₁, r₂, etc. est encore une loi binomiale négative, de paramètres p et r = r₁ + r₂. Cette propriété provient de l'expression de la fonction génératrice des moments et peut se généraliser à la somme de n variables.