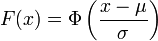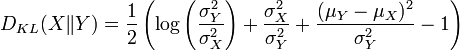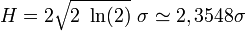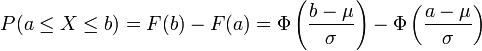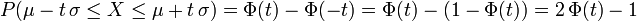Loi normale - Définition
La liste des auteurs de cet article est disponible ici.
Champ d'application
Le Théorème de Moivre-Laplace affirme la convergence d'une loi binomiale vers une loi de Gauss quand le nombre d'épreuves augmente. On peut alors utiliser la loi normale comme approximation d'une loi binomiale de paramètres (n ; p) pour n grand et p, 1 - p de même ordre de grandeur ; on approche alors cette loi binomiale par la loi normale ayant même espérance np et même variance np(1 − p).
On a dessiné ci-dessous :
- la loi binomiale de paramètres (12;1 / 3) (diagramme en bâtons rouge) et la loi normale correspondante d'espérance 4 et de variance 8 / 3 (courbe verte)
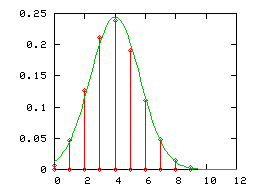
- la loi binomiale de paramètres (60;1 / 3) (diagramme en bâtons rouge) , et la loi normale correspondante d'espérance 20 et de variance 40 / 3 (courbe verte)
Le mathématicien Carl Friedrich Gauss a introduit cette loi pour le calcul d'erreurs.
En statistiques, de nombreux phénomènes suivent des distributions gaussiennes : données biométriques des individus (Adolphe Quetelet).
La loi normale générale
Soient
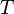
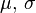
 .
.
On définit la variable aléatoire
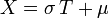
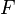
On a
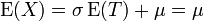
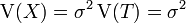
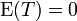
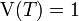
Cherchons la loi de
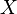
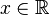
-
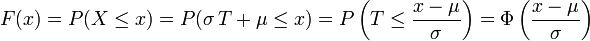
- puisque la fonction de répartition de
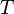
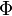
Ainsi,
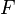
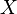
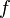
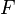
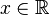
-
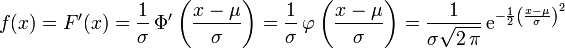
Ceci légitime la définition suivante :
Définition
On appelle loi normale (ou gaussienne, ou de Laplace-Gauss) de paramètres
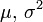
 ) la loi de probabilité définie par la densité
) la loi de probabilité définie par la densité
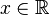
-
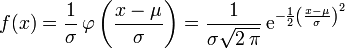
Une variable gaussienne est une variable aléatoire réelle qui suit une loi normale de paramètres
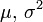
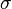
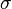
Notation: cette loi est notée
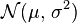
La loi normale centrée réduite est notée
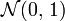
On peut énoncer plusieurs propriétés, compte tenu de ce qui précède (le dernier point se démontrant de manière analogue).
Propriétés
Soit une variable aléatoire
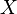
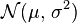
- son espérance et sa variance existent et
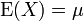

- sa fonction de répartition
- la variable aléatoire
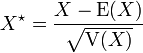
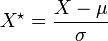
- si
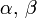
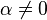
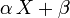
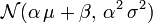
Soit une variable aléatoire
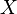
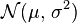
- son espérance existe et vaut
![\ \mathrm{E}[\exp(X)] = \exp\left( \mathrm{E}(X) + \frac{\mathrm{V}(X)}{2}\right) = \exp\left(\mu + \frac{\sigma^2}{2}\right)](https://static.techno-science.net/illustration/Definitions/autres/3/30291b6746a216f9aea6087c3440c29c_199cba7cc620c837212d0e9b75a98cbd.png)
- sa variance existe et vaut
![\ \mathrm{V}[\exp(X)] = \exp( 2 \mathrm{E}(X) + \mathrm{V}(X)) \left[\exp( \mathrm{V}(X)) - 1\right] = \exp( 2 \mu + \sigma^2) (\exp(\sigma^2) - 1)](https://static.techno-science.net/illustration/Definitions/autres/f/f7f3fc868964a3688295009b3f518506_0d222e8346b30d58f83f27fbe22b9407.png)
Soit une variable aléatoire
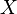
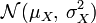
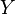
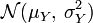
Largeur à mi-hauteur
Lorsque l'on travaille sur une représentation graphique, on estime fréquemment la largeur de la gaussienne par sa largeur à mi-hauteur H (en anglais full width at half maximum, FWHM), qui est la largeur de la courbe à une altitude qui vaut la moitié de l'altitude du sommet. La largeur à mi-hauteur est proportionnelle à l'écart type :
Le facteur 2 sert à prendre en compte l'extension de la gaussienne dans les valeurs négatives.
Calcul de P(a ≤ X ≤ b)
Les résultats précédents permettent de ramener tout calcul de probabilité relatif à la loi normale
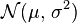
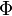
Si la variable aléatoire
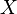
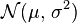
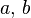
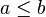
Cas d'un intervalle centré à la moyenne, plages de normalité
- Si t est un réel positif,
- lorsque
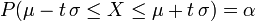
![\ \alpha \in\, ]0,\, 1[](https://static.techno-science.net/illustration/Definitions/autres/e/ebf510469db31b72eca5620b9c1f2eb6_6337c44e3c97e04b3388365f240b3460.png)
- ce qui équivaut à
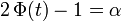
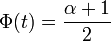
- l'intervalle
![\ [\mu - t\, \sigma,\, \mu + t\, \sigma] = [\mathrm{E}(X) - t\, \sigma,\, \mathrm{E}(X) + t\, \sigma]](https://static.techno-science.net/illustration/Definitions/autres/7/73254f7af8bf0426f9279822faf6dcd5_6456326cd5d644dccb5615fef7bdebfc.png)
- (si par exemple, α = 0,95, on dit : "plage de normalité au niveau de confiance 95%" : en statistique, c'est un intervalle dans lequel se trouve 95% de la population lorsque la distribution est gaussienne).
Exemples numériques
Grâce à la table précédente, on obtient :
-
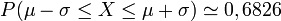
- l'intervalle
![[\mathrm{E}(X) - \sigma,\, \mathrm{E}(X) + \sigma]](https://static.techno-science.net/illustration/Definitions/autres/1/1897c506e498c1c9c7de0dc2fc0819b5_a6af3a57d057f1c4df90e1fbc96d2136.png)
-
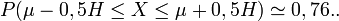
- l'intervalle
![[\mathrm{E}(X) - 0,5H,\, \mathrm{E}(X) + 0,5H]](https://static.techno-science.net/illustration/Definitions/autres/6/673ab2373f88c2a93e126c2f1b15d9bc_ed8c8fb919737cfde68975b6924e96de.png)
-
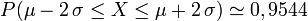
- l'intervalle
![[\mathrm{E}(X) - 2\, \sigma,\, \mathrm{E}(X) + 2\, \sigma]](https://static.techno-science.net/illustration/Definitions/autres/3/3cbacb02bf77d378a8d28a903520c815_d97d3aaeb13b64625a7e35345759b565.png)
-
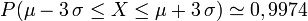
- l'intervalle
![[\mathrm{E}(X) - 3\, \sigma,\, \mathrm{E}(X) + 3\, \sigma]](https://static.techno-science.net/illustration/Definitions/autres/0/0a0ea77659ca495de15d3b31c79d44c2_72edab94f0b6b89506f1ac5a5ebb0055.png)