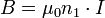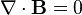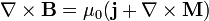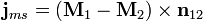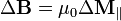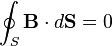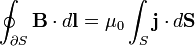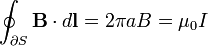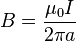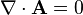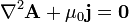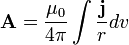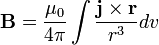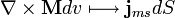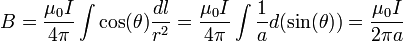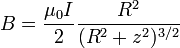Magnétostatique - Définition

Approche ampérienne

L’approche ampérienne s’attache au calcul de B. Elle est actuellement privilégiée dans l’enseignement car elle est proche de l’électromagnétisme dans le vide. Les équations à résoudre sont :

On peut remarquer que le terme ∇×M dans la deuxième équation agit comme un courant supplémentaire, ce qui lui a valu d’être interprété comme une densité de courant microscopique (appelée courant lié) découlant du mouvement des électrons dans leurs orbites atomiques. Cette interprétation classique d’un phénomène quantique a cependant ses limites : si elle décrit assez bien le magnétisme découlant du moment cinétique orbital, elle ne rend pas bien compte de celui lié au spin des électrons.

En pratique, l’approche ampérienne est privilégiée dans les situations où il n’y a pas de matière aimantée et le champ est dû exclusivement au courant. Nous nous placerons par la suite dans ce cas où on a alors ∇×B = μ₀ j. Pour retrouver le cas général (en présence de matière aimantée) il suffit de remplacer j par j + ∇×M.

Courants liés de surface

Il arrive souvent qu’on ait affaire à des systèmes présentant des surfaces où l’aimantation est discontinue. Par exemple, si un aimant avec aimantation uniforme est plongé dans le vide, l’aimantation à la surface de l’aimant passe de façon discontinue d’une valeur finie (à l’intérieur) à zéro (à l’extérieur). Dans ce cas, la densité de courant lié ∇×M peut être infinie. Dans un tel cas on remplace à la surface la densité volumique de courant lié par une densité surfacique :

où M₁ et M₂ sont les aimantations de chaque côté de la surface de discontinuité et n₁₂ est le vecteur unitaire normal à cette surface, orienté de 1 vers 2. L’effet sur le champ de ce courant surfacique est d’induire une discontinuité de B :

où

• ΔM et ΔB représentent les discontinuités de M et B (comptées dans le même sens) ;
• ΔM_∥ représente la partie de ΔM qui est parallèle à la surface.

Cette discontinuité n’affecte que la partie de B parallèle à la surface. La partie normale de B reste quant à elle continue.

Relations intégrales

Deux relations intéressantes peuvent être obtenues en appliquant le théorème de Stokes aux relations locales. La relation ∇⋅B = 0 nous donne :

où l’intégrale, qui s’étend sur une surface fermée S, est le flux sortant de B. Il s’agit du théorème de flux-divergence. L’autre relation s’obtient en intégrant ∇×B = μ₀j sur une surface ouverte S :

où l’intégrale de gauche est la circulation de B sur le contour de S. Cette relation est connue sous le nom de théorème d'Ampère. Le membre de droite s’interprète simplement comme le courant traversant la surface.

Ces relations intégrales permettent souvent de calculer B simplement dans les situations de haute symétrie.

Exemple

Soit à calculer le champ crée par un conducteur rectiligne infini. Des considérations de symétrie donnent l’orientation du champ : celui-ci tourne dans des plans perpendiculaires au fin conducteur. Son module peut être calculé en appliquant le théorème d’Ampère à la surface S délimitée par une ligne de champ de rayon a :

où I est le courant transporté par le fil. On en déduit le module de B :

On voit que le champ décroît en proportion inverse de la distance au fil.

Potentiel vecteur

La divergence de B étant nulle, on peut faire dériver B d’un potentiel vecteur A :

Pour assurer l’unicité de A, on le contraint en général à respecter la jauge de Coulomb :

Moyennant quoi, A est solution de l’équation de Poisson :

Solution intégrale

On peut montrer que A est donné par l’intégrale

où l’intégrale s’étend à tout l’espace (ou du moins aux zones où j ≠ 0) et

• r désigne la distance entre le point courant de l’intégrale et celui où A est calculé ;
• dv est l’élément de volume.

De la même manière, B est donné par

où

• r est le vecteur allant du point courant de l’intégrale à celui où B est calculé ;
• r est le module de r.

Cette dernière relation est connue sous le nom de loi de Biot et Savart.

Dans le cas où il y a de la matière aimantée, il faut bien sûr tenir compte des courants liés en remplaçant j par j + ∇×M. En présence de courants liés de surface, il faut ajouter aux intégrales de volume des intégrales de surface qui se déduisent des précédentes par la substitution

Une situation rencontrée couramment est celle où le courant circule dans un circuit filiforme, et où on néglige la section du fil. Dans ce cas, les intégrales volumiques pour A et B sont remplacées par des intégrales linéiques le long du fil moyennant la substitution

où I est le courant dans le fil et dl l’élémént de longueur, orienté selon I.

Exemples

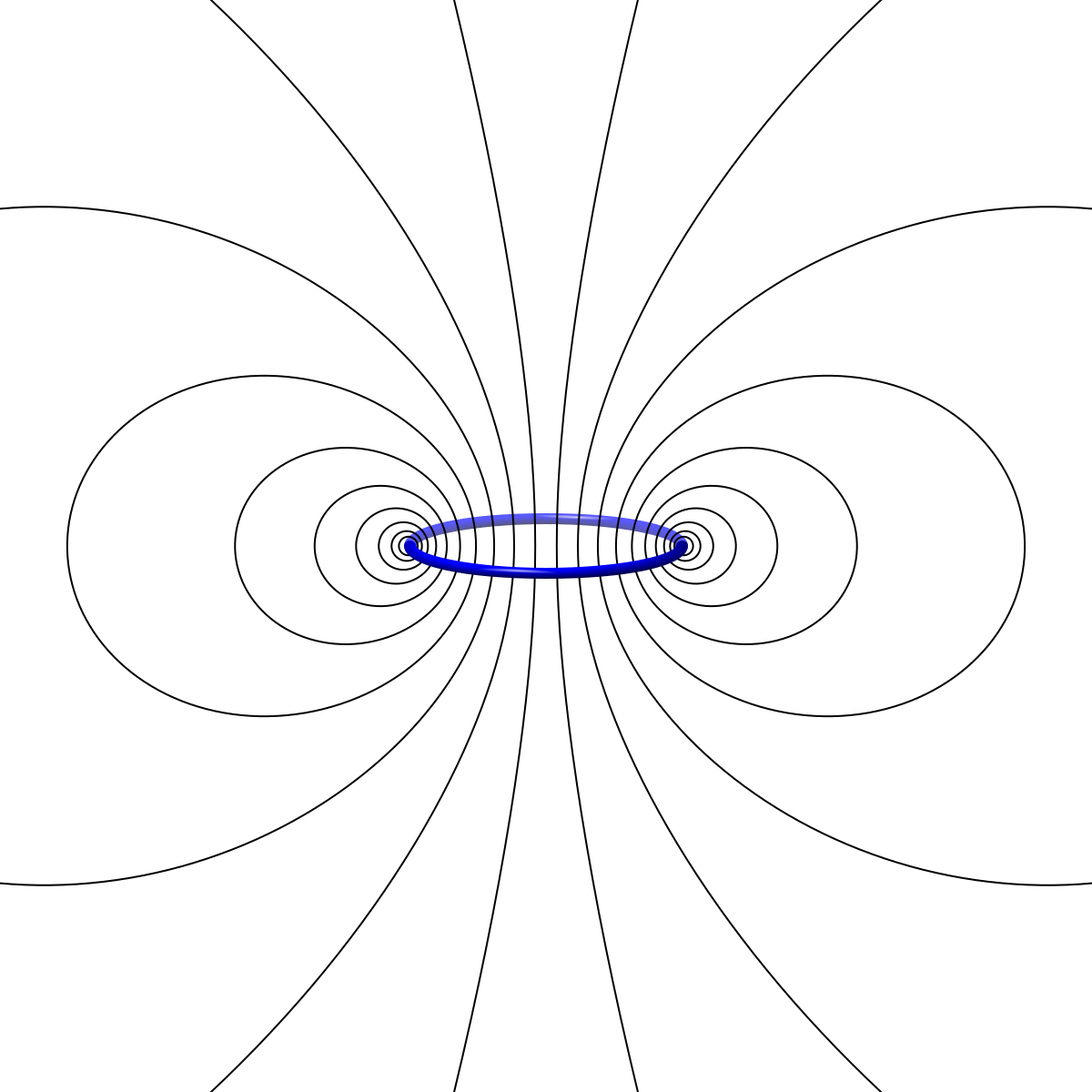
Fil infini :

On peut reprendre l’exemple précédent et calculer le champ créé par un fil infini avec la loi de Biot et Savart :

Autres exemples :

• Champ créé sur l’axe d’une spire circulaire de rayon R :

• Champ créé par un solénoïde infiniment long :

à intérieur du solénoïde, le champ étant nul à l’extérieur. La quantité n₁ désigne le nombre de spires par unité de longueur.