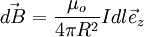Spire de courant - Définition
En électromagnétisme, on appelle spire de courant un circuit électrique fermé parcouru par un courant électrique. Le circuit le plus simple étant un cercle (aussi appelé boucle) pour lequel le mouvement d'ensemble des électrons est circulaire. En pratique, une telle spire peut être obtenue avec un fil électrique en forme de cercle alimenté par une pile électrique. Un ensemble de spires de courant disposées côte à côte constitue une bobine électrique ou solénoïde. On peut aussi considérer que le mouvement d'un électron autour d'un atome est circulaire[1], et correspond donc, de manière imagée, à une spire de courant.
Propriétés générales
- Lorsque le fil électrique qui la constitue est traversé par un courant électrique, une spire de courant produit un champ magnétique, c'est la base de l'électroaimant.
- Lorsqu'une spire de courant est placée dans un champ magnétique variable, un courant électrique est induit dans la spire selon la Loi de Lenz.
- Lorsqu'une spire de courant est parcourue par un courant électrique et placée dans un champ magnétique, elle s'oriente par l'effet de la force de Laplace de façon à maximiser le flux qui la traverse.
Calcul du champ magnétique
L'effet principal d'une spire de courant est de créer dans son voisinage un champ magnétique de forme relativement complexe. Toutefois, comme de nombreux phénomènes physiques font intervenir ce type de spires, il est intéressant de le connaître. Par exemple, il permet de calculer les champs magnétiques créés dans un solénoïde ou dans des bobines d'Helmholtz, ou encore de comprendre la notion de dipôle magnétique. Dans tous les cas, le phénomène n'est jamais parfaitement circulaire : il est modélisé par la notion de spire circulaire de courant.
On note R le rayon de la spire et I le courant la parcourant. On cherche à calculer le champ magnétique
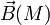
Cas d'un courant constant
En supposant que le courant I ne varie pas dans le temps, le problème vérifie alors les lois de la magnétostatique. On peut alors expliciter une propriété générale : les antisymétries du système permettent de montrer que le champ
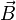
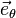
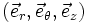
-
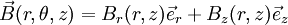
L'axe Oz étant l'intersection des plans d'antisymétrie le champs pour M sur Oz est dirigé suivant Oz axe de la spire.
Champ au centre O de la spire
La loi de Biot et Savart est relativement simple à appliquer au centre O de la spire. En effet, il suffit de sommer la contribution
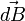
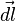
où μ0 est la perméabilité magnétique du vide.
En faisant la somme de chacune de ces contributions, on obtient :
-
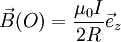
On peut remarquer que ce champ, comme on aurait put le prévoir, augmente lorsqu'on élève la valeur du courant et lorsque le rayon de la spire diminue.
Par exemple, pour un courant de 0,1 ampères parcourant une spire de rayon 1 centimètre, cela donne un champ magnétique d'environ 10-5 Teslas. Pour augmenter cette valeur, un méthode simple est d'effectuer plusieurs tours avec le fil électrique : c'est le principe des bobines et du solénoïde.
Champ sur l'axe de la spire
Pour obtenir la valeur du champ sur l'axe de la spire en un point M tel que OM = z, il faut utiliser la même méthode que pour le paragraphe précédent, c'est-à-dire additionner les champs créés par des éléments de la spire. En définissant l'angle θ par tan(θ) = z / R, on obtient le résultat suivant :
-
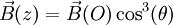
Cette expression montre que, sur l'axe de la spire, le champ créé diminue lorsqu'on s'éloigne du centre O. Plus précisément, à une distance z très grande devant R, on obtient la relation :
-
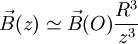
On retrouve ainsi une forme analogue au dipôle magnétique.
Champ loin de la spire
Dans ce cas on peut retrouver l'expression obtenue pour un moment dipolaire magnétique.
Cas d'un champ oscillant
On retrouve l'expression d'un dipôle magnétique oscillant.