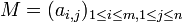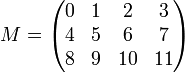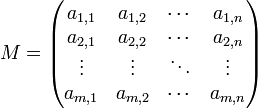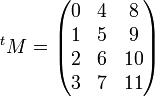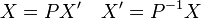Matrice (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, les matrices servent à interpréter en termes calculatoires et donc opérationnels les résultats théoriques de l'algèbre linéaire et même de l'algèbre bilinéaire. Toutes les disciplines étudiant des phénomènes linéaires utilisent les matrices. Quant aux phénomènes non linéaires, on en donne souvent des approximations linéaires comme c'est le cas en optique géométrique avec les approximations de Gauss.
Définitions
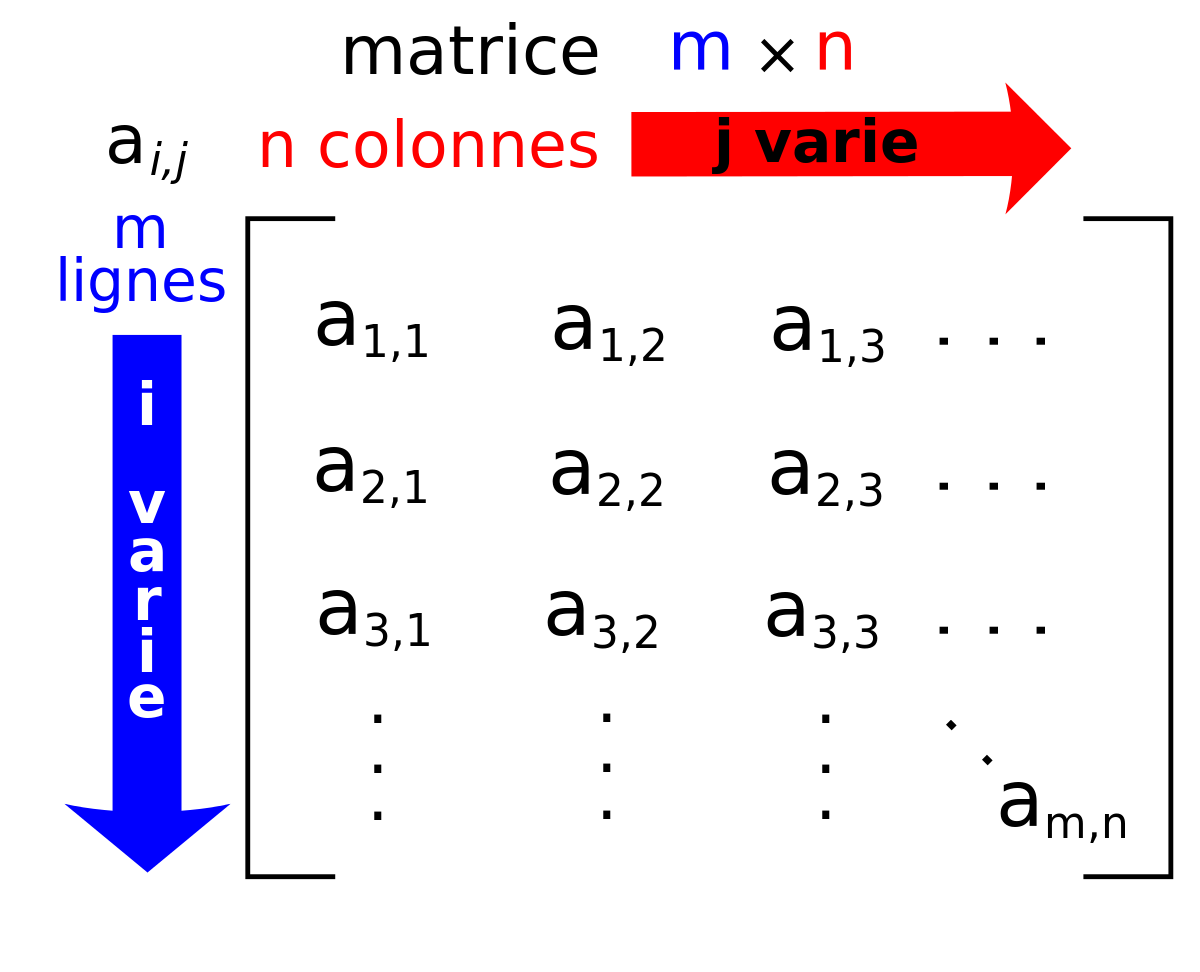
Une matrice à m lignes et n colonnes est un tableau rectangulaire de mn nombres, rangés ligne par ligne. Il y a m lignes, et dans chaque ligne n nombres.
Passons maintenant à la définition formelle. Soient A un ensemble et (m,n) un couple d'entiers positifs. Le plus souvent, l'ensemble A est muni d'une structure de corps commutatif mais on utilise aussi fréquemment des matrices à coefficients dans un anneau.
On appelle matrice à coefficients dans A, de dimension (ou taille) (m,n) (c'est-à-dire à m lignes et n colonnes), une famille (ai,j) d'éléments de A indexée par le produit cartésien des ensembles de nombres entiers [1,m] et [1,n].
La matrice M pourra être notée par
ou plus simplement (ai,j) si le contexte s'y prête.
On représente généralement une matrice sous la forme d'un tableau rectangulaire. Par exemple, est représentée ci-dessous une matrice M, à coefficients entiers, et de dimension (3,4) :
Dans cette représentation, le premier coefficient de la dimension est le nombre de lignes, et le deuxième, le nombre de colonnes du tableau. Une matrice pour laquelle le nombre m de lignes est égal au nombre n de colonnes sera dite matrice carrée de taille n. Une matrice ne comportant qu'une seule ligne et n colonnes est appelée matrice ligne de taille n. Une matrice ne comportant m lignes et une seule colonne est appelée matrice colonne de taille m.
Pour repérer un coefficient d'une matrice, on indique son indice de ligne puis son indice de colonne, les lignes se comptant du haut vers le bas et les colonnes de la gauche vers la droite. Par exemple, on notera ai,j, les coefficients de la matrice M, pour
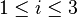
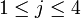
La disposition générale des coefficients d'une matrice M de taille (m,n) est donc la suivante
Pour effectuer certaines opérations, il peut être utile de travailler sur le système des lignes ou des colonnes d'une matrice. On pourra alors l'écrire sous une des formes suivantes
-
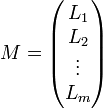

L'ensemble des matrices à coefficients dans A possédant m lignes et n colonnes est noté Mm,n(A) (ou parfois M(m,n,A)).
Lorsque m=n on note plus simplement Mn(A).
Soit
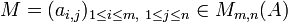
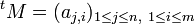
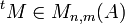
Par exemple, avec la matrice M des exemples précédents, on a
L'opération de transposition est involutive, c'est-à-dire que
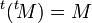
Interprétations linéaires
Un intérêt principal des matrices est qu'elles permettent d'écrire commodément les opérations habituelles de l'algèbre linéaire, avec une certaine canonicité.
Coordonnées
Le premier point est de remarquer que le A-module An s'identifie canoniquement à l'espace de matrices colonnes Mn,1(A) : si ei est le n-uplet dont tous les coefficients sont nuls, sauf le i-ème qui vaut 1, on lui associe la matrice colonne élémentaire dont tous les coefficients sont nuls sauf le i-ème qui vaut 1, et on étend l'identification par linéarité ; la matrice associée à chaque n-uplet sera appelée matrice coordonnée canonique.
D'autres identifications sont cependant possibles ; lorsqu'on peut parler de base (si l'anneau des scalaires est un corps, ou est principal, par exemple), on peut associer les matrices colonnes élémentaires à n'importe quelle base de l'espace An (ou plus généralement d'un A-module libre), puis à nouveau étendre par linéarité ; les matrices associées seront appelées matrices coordonnées dans la base envisagée.
On peut concaténer les matrices coordonnées, dans une base fixée, de plusieurs n-uplets. On obtient ainsi la matrice coordonnée d'une famille de vecteurs. Le rang de la matrice est alors défini comme la dimension de la famille de ces vecteurs. En particulier la matrice d'une base dans une autre base est appelée matrice de passage entre ces deux bases, ou matrice de changement de base. Si X et X' sont les matrices coordonnées du même vecteur dans deux bases B et C, et que P est la matrice de la base C dans la base B, on a la relation (une matrice de passage est toujours inversible) :
Applications linéaires
Soient E et F deux A-modules (à gauche) libres de dimensions finies. Soit B=(e1,...,ep) une base de E et C=(f1,...,fn) une base de F. Soit enfin φ une application linéaire de E dans F.
On appelle matrice de φ dans le couple de bases (B,C) la matrice :
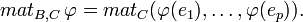
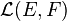

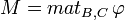
Soit x un vecteur de E. Notons
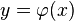
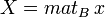
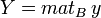
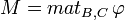
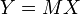
Cette formule devient
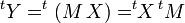
L'application
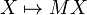
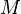
En conséquence, il arrive souvent que l'on l'identifie avec l'application linéaire ci-dessus. On parlera alors de noyau de la matrice, d'espaces propres de la matrice, d'image de la matrice, etc.
Si E et F sont deux A-modules, B et B' deux bases de E, de cardinal p, et C et C' deux bases de F de cardinal n,
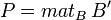

-
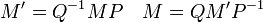
On constate ainsi que deux matrices équivalentes, d'après la définition donnée plus haut dans l'article, sont deux matrices qui représentent la même application linéaire dans des bases différentes.
En particulier, dans le cas d'un endomorphisme, si on impose B= B' et C=C' , les formules précédentes se simplifient :
On constate ainsi que deux matrices semblables, d'après la définition donnée plus haut dans l'article, sont deux matrices qui représentent le même endomorphisme dans des bases différentes.