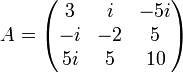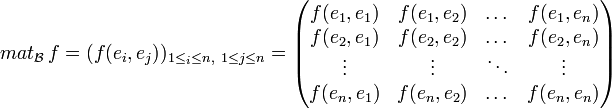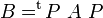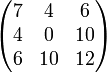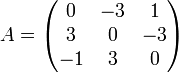Matrice (mathématiques) - Définition

Décomposition d'une matrice

• On utilise abusivement le terme décomposition d'une matrice, qu'il s'agisse d'une véritable décomposition (en somme) comme dans la décomposition de Dunford ou d'une factorisation comme dans la plupart des autres décompositions.

Réduction d'une matrice carrée

• Réduire une matrice, c'est trouver une matrice qui lui est semblable la plus simple possible.
• Une matrice diagonalisable est une matrice semblable à une matrice diagonale.

A est diagonalisable si et seulement s'il existe une matrice inversible P et une matrice diagonale D telles que A = P ^{− 1}DP.

• Sur un corps algébriquement clos, on dispose de la réduction de Jordan qui est optimale et il existe des décompositions intermédiaires comme la décomposition de Dunford qui utilise les sous-espaces caractéristiques ou celle de Frobenius qui utilise les sous-espaces cycliques.
• Les polynômes d'endomorphismes jouent un rôle crucial dans les techniques de réduction.

Décomposition LU

• C'est une factorisation en produit de deux matrices triangulaires.
• En lien avec le pivot de Gauss, c'est une méthode qui permet d'inverser une matrice.

Décomposition QR

• C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
• C'est une factorisation en produit d'une matrice orthogonale et d'une matrice triangulaire.
• C'est une traduction matricielle du procédé de Gram-Schmidt.

Décomposition polaire

• C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
• C'est une factorisation en produit d'une matrice orthogonale et d'une matrice symétrique strictement positive dans le cas réel, en produit d'une matrice unitaire et d'une matrice hermitienne strictement positive dans le cas complexe.
• On peut décomposer à droite ou à gauche.
• On a unicité de la factorisation pour les matrices inversibles.

Interprétations bilinéaires

Dans ce paragraphe, l'anneau commutatif des scalaires sera noté . Dans la plupart des applications, ce sera un corps commutatif.

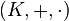
Le cas non commutatif existe aussi mais il faut prendre quelques précautions et les notations deviennent trop lourdes pour cet article.

Matrice d'une forme bilinéaire

Soit E un K-module libre et une base de E.

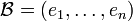
Soit une forme bilinéaire. On définit la matrice de f dans la base par la formule suivante :

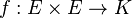
Dans le cas particulier où et f est un produit scalaire, cette matrice est appelée matrice de Gram.

est symétrique (respectivement antisymétrique) si et seulement si f est symétrique (respectivement antisymétrique).

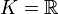
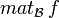
Soit x et y deux vecteurs de E. Notons X et Y leurs coordonnées dans la base et . On a alors la formule : f(x,y) = ^tXAY.

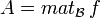
Deux formes bilinéaires sont égales si et seulement si elles ont la même matrice dans une base donnée.

Matrice d'une forme quadratique

Lorsque est un corps de caractéristique différente de 2, on appelle matrice d'une forme quadratique la matrice de la forme bilinéaire symétrique dont est issue la forme quadratique.

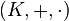
Formule de changement de base

Soit E un K-module libre, et deux bases de E. Soit une forme bilinéaire.

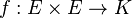
Notons la matrice de f dans la base et la matrice de f dans la base . Notons la matrice de passage. On a alors :

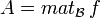
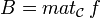
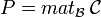
Matrices congruentes

Deux matrices carrées A et B sont dites congruentes s'il existe une matrice inversible P telle que A = ^tPBP.

Deux matrices congruentes sont deux matrices qui représentent la même forme bilinéaire dans deux bases différentes.

Lorsque est un corps de caractéristique différente de 2, toute matrice symétrique est congruente à une matrice diagonale. L'algorithme utilisé s'appelle réduction de Gauss à ne pas confondre avec le pivot de Gauss.

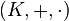
Matrices orthogonales

Matrices unitaires

Matrices symétriques

En algèbre linéaire, une matrice symétrique est une matrice qui est égale à sa propre transposée.

Exemple :

Matrices antisymétriques

En algèbre linéaire, une matrice carrée A est dite antisymétrique si sa transposée est égale à son opposée ; c'est-à-dire si elle satisfait à l'équation : ^tA = -A

Exemple

Ici, la matrice A est antisymétrique :

Matrice d'une forme sesquilinéaire

Matrices hermitiennes

Une matrice A est dite hermitienne si .

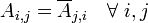
Exemple

est une matrice hermitienne.

Matrices quaternioniques