Nicolas Chuquet - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Nicolas Chuquet, né entre 1445 et 1455 à Paris, mort entre 1487 et 1488 à Lyon, est un mathématicien français.
Biographie
Arrivé à Lyon vers 1480, on ne savait plus de sa vie en 1880 que ce qu'il en avait raconté dans son livre sur la science des nombres. Les travaux de J. Itard, après ceux d'Aristide Marre, de Tannerey et de Lambo permettent de tracer un portrait plus complet du mathématicien le plus inventif de la fin du moyen-âge occidental.
Parisien, Bachelier en médecine, Nicolas Chuquet a publié à Lyon en 1484 son œuvre majeure, écrite en français Triparty en la science des nombres. Il y affirme :
- Et ainsi a l'honneur de la glorieuse trinité se termine ce livre lequel pour raison de ces trois parties générales je l'appelle triparty. Et aussi pour cause quil a été fait par Nicolas Chuquet, parisien, Bachelier en medecine. Je le nomme triparty de Nicolas en la science des nombres. Lequel fut composé medié et fini à Lyon sus le Rhône l'an de salut 1484.
Par malheur, cette œuvre majeure, Triparty en la science des nombres, ne fut jamais publiée de son vivant.
La première trace qu'on ait de lui date du quatre juin 1484 ; il est enregistré comme écrivain (celui qui enseigne aux enfants à écrire) et habite entre la Porte des Frères Mineurs et la rue de la Grenette vers le Muton, soit dans l'actuelle rue de la République. Il y demeure encore 5 ans plus tard, sous le nom d'algoriste, et on l'y retrouve en 1487. D'après Hervé L'Huillier, c'est un quartier de petites gens ; ses voisins sont des panetiers, un toilier, un couturier, des sergents, et son niveau de fortune est encore inférieur au leur. On pense qu'il meurt en 1488.
Un manuscrit datant de 1470 et rédigé sur un papier italien confirme l'idée que Chuquet venait d'italie, ou tout au moins était influencé par la culture italienne, notamment au travers des œuvres de Luca Pacioli ; son œuvre pouvant se comparer à la Summa de geometrica, arithmetica, proportioni et proportionalita, éditée en 1494 par ce dernier. Estienne de La Roche, puis Gilles Hughetan, dans l'édition qu'ils ont donné de L'Arismethique nouvellement composée ont indiqué leurs dettes envers Paccioli et Philippe Friscobaldi (un banquier de Lyon né à Florence), sans mentionner ce qu'ils devaient à Chuquet.
Parmi les livres d'arithmétique qui ont influencé Chuquet, on relève généralement le Compendy de la praticque des nombres, issu du Manuscrit de Cesena attribué à Barthélemy de Romans, frère Prêcheur, copié en 1476 à Lyon par Mathieu Préhoude et l'algorithme de Pamiers. On note aussi parmi les précurseurs de Chuquet dont il semble que celui-ci ait eu connaissance Fibonacci et son liber abaci. Ces influences ne font toutefois pas l'unanimité.
Larismethique de Chuquet
L'Œuvre
Triparty, comme son nom l'indique, est divisé en trois parties :
- Première partie : Traité des nombres entiers ; Traité des nombres rompus, ou fractions ; Des progressions, des nombres parfaits, des nombres proportionnels et de leurs propriétés ; 4 Règles de trois, d'une ou deux positions, règle des nombres moyen .
- Seconde partie : Des racines simples, composées, liées (six chapitres)
- Tierce et dernière partie : Règle des premiers ; Excellence de cette règle qui est la clef, l'entrée et la porte des abîmes qui sont en la science des nombres (trois chapitres).
Dans cet ouvrage, dont on retient le plus souvent l'aspect ludique, Chuquet donne les premières règles algébriques jamais écrites en français. À partir des exposants, tout autrement employés avant lui par Nicole Oresme, il invente un symbolisme algébrique nouveau et pressent, au cours de ses travaux, l’existence des logarithmes.
Chuquet y donne :
- la méthode d’extraction des racines carrées à la main ;
- l'écriture
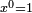
- la règle de trois et son explication ;
- la règle de la chose, la règle des nombres premiers ;
- la méthode de la fausse position ;
- un sens à des quantités négatives par l'emploi de signes

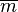
- deux solutions aux équations du second degré ;
- La notation R pour racine.
Un novateur
La pensée de Chuquet est brillante et très en avance sur son temps. Il invente sa propre notation pour les concepts algébriques et les exponentiations. Il semble avoir été le premier mathématicien à avoir reconnu le zéro et les nombres négatifs comme exposants.
On lui doit également notre système actuel de grands nombres : million, billion, trillion, etc., mais surtout d'avoir approché de fort peu, cent ans avant Bombelli, l'existence des nombres complexes : résolvant une équation du second degré et obtenant comme solution
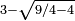
Les grands nombres
Le mot « million » (signifiant "le grand mille", donc bien notre million) a été en usage longtemps avant Chuquet. On fait remonter son invention vers 1270. Jehan Adam enregistra les mots « bymillion » et « trimillion » pour 1012 et 1018 en 1475 ; et il est admis que ces mots ou d'autres similaires étaient d'un usage général à cette période. Nicolas Chuquet fut, néanmoins, l'auteur original du premier usage d'une série de noms, étendus et systématiques en -illion ou -yllion.
C'est pourquoi, le système dans lequel les noms million, billion, trillion, etc. font référence aux puissances d'un million est nommé le système Chuquet.
À la fin du premier chapitre de son ouvrage « Triparty en la science des nombres » Nicolas Chuquet écrit:
- "Ou qui veult le premier point peult signiffier million, le second point byllion, le tiers point tryllion, le quart quadrillion, le cinquième quyllion, le sixième sixlion, le septième septyllion, le huytième ottyllion, le neufième nonyllion et ainsi des aultr's se plus oultre on vouloit proceder. Idem lon doit sauoir que ung million vault mille milliers de unitez, et ung byllion vault mille milliers de millions. Et tryllion vault mille milliers de byllions. Et ung quadrillion vault mille millier de tryllions et ainsi des ault’s. Et de ce en est pose ung exemple nombre diuise et ponctoye ainsi que devant est dit. Tout le quel nombre monte: 745324 trillion, 804300 byllions, 700023 millions, 654321. Exemple: 745324' 804300' 700023' 654321."
Demeuré à l'état de manuscrit, le travail de Chuquet n'eut qu'une influence indirecte sur cette notation, son travail n'étant publié qu'après 1870, mais la copie qu'en avait fait La Roche dans une partie de « L'arismetique » contribua de façon déterminante à l'adoption de son système.
Lorsqu'au début du dix-septième siècle, on commença – pour une meilleure lisibilité – de diviser les grands nombres en groupes de trois au lieu de groupes de six, on adopta le terme « milliard » (Jacques Pelletier du Mans, 1550) pour 10 ; une idée qui remonterait à Guillaume Budé. On distingua dès lors l'Échelle longue, ou système Chuquet-Pelletier, le système de noms numériques dans lequel le mot billion signifie un million de millions, de l'Échelle courte, système de noms numériques dans lequel le mot billion signifie un millier de millions en totale opposition avec les idées de Chuquet.
Une véritable guerre oppose depuis le XVIIe siècle les tenants des deux échelles
| échelle courte | Base 10 | Puissance | Chuquet | Pelletier | Préfixe SI |
|---|---|---|---|---|---|
| | | million 0 | | | |
| | | million 0.5 | | | |
| | | million 1 | | | |
| | | million 1.5 | | | |
| | | million 2 | | | |
| | | million 2.5 | | | |
| | | million 3 | | | |
| | | million 3.5 | | | |
| | | million 4 | | | |
Les États-Unis ont adopté l'échelle courte au XIXe siècle sur les conseils d'encyclopédistes français... À leur suite les milieux financiers et le bureau international des poids et mesures. La France, après avoir hésité tout au long du dix-neuvième siècle, confirma en 1961 par le Journal officiel l'usage de l'échelle longue. En 1974, Harold Wilson fit passer l'Angleterre sur l'échelle courte ; toutefois en 1994, l'Italie confirma son adoption de l'échelle longue, à laquelle demeure attachée la majorité des pays non anglophones (Brésil excepté).
Nommer du nom de Chuquet un système où n'apparaît que les billions, les trillions et les quintillions pour désigner 109,1012,1015mais ni les milliards ni les billiards alors que, jusqu'à preuve du contraire, Chuquet n'a jamais noté de la sorte les puissances du million relève d'une interprétation assez large, et probablement erronée, de l'œuvre du grand algébriste.


















































