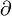Notations delta en sciences - Définition

d (lettre d minuscule)

Une grandeur ne varie pas forcément à un rythme constant. Par exemple, un enfant grandit de moins en moins vite, puis sa taille se stabilise. De même, la pente d'une route n'est pas constante : il existe, le long d'un trajet, une succession de côtes, de descentes et de plats ; par ailleurs, une pente peut comporter en réalité différentes portions plus ou moins pentues ; etc.

La lettre d minuscule représente une petite variation, sur un court instant ou entre deux points proches. Il s'agit donc toujours d'exprimer un écart, ou une différence, ou une variation, mais cette fois de façon locale et non plus globale. L'échelle locale dépend de l'échelle globale : pour une ville d'un kilomètre de circonférence, une distance de 200 m est certainement plutôt un écart d'échelle globale, mais si on considère la Terre (rayon = 6400 km), cette même distance est très petite et de l'ordre de l'échelle locale.

Si on considère par exemple une fonction f appliquée à une variable x, si on souhaite expliciter une pente locale (c'est-à-dire un taux d'accroissement localisé), il ne faut pas considérer une variation Δx quelconque mais la prendre « la plus petite possible », ce qui en mathématiques revient à faire tendre cette variation vers zéro (voir aussi la notion de limite et de dérivée). On dit alors que dx est un infinitésimal : l'écart qu'il représente est très petit par rapport à l'échelle du problème, et au mieux, infiniment petit.

Cette notion de variation locale possède également des applications concrètes. Physiquement, elle dépend beaucoup du contexte. Dans l'exemple précédent du code de la route, la pente indiquée par les panneaux routier correspond en fait à la pente des prochains mètres, et non à la variation d'altitude sur tout le trajet. Cette information, rapportée à l'échelle de longueur du trajet tout entier, est donc considérée comme locale.

Pour indiquer cette notion de « petite variation » ou de « variation infinitésimale », on modifie la notation en utilisant d au lieu de Δ. Le choix de l'une ou l'autre des deux notations dépend uniquement du ratio d'échelles (échelle du problème versus échelle de la variation). Ainsi, pour définir la vitesse, prenons un trajet d'une heure (on note Δt = 1 h) entre deux villes distantes de ΔL = 50 km. La vitesse moyenne (écart global de distance sur écart global de temps) aura été de ΔL/Δt = 50 km/h, qu'on pourrait noter Vmoyenne. Localement, toutefois, la vitesse n'aura pas nécessairement été constante : tout au long du trajet, le véhicule a accéléré et ralenti. On peut alors s'intéresser à la vitesse « instantanée » (à un instant précis du trajet), c'est-à-dire pendant un « très court moment » : sur cet « écart infinitésimal » de temps, la vitesse pouvait être de 60 km/h au compteur, soit 1 km par minute (environ 17 m par seconde). On noterait alors : dL/dt = 17 m/s = 60 km/h = Vréelle. Cette information différente n'est valable que localement, autour du point considéré pour effectuer le calcul.

En résumé

L'usage des notations delta se rapporte à chaque fois à l'expression soit d'une variation, soit d'une petite quantité locale ou élémentaire. Ceci peut se faire à grande ou petite échelle (variation et quantité infinitésimales) et une ou plusieurs variables peuvent intervenir dans la détermination des variations d'une grandeur. Les différentes notations utilisées permettent de garder à l'esprit ce que représente dans un certain contexte ces différents éléments : considère t-on une variation ? partielle ou totale, globale ou locale ? ou bien une quantité élémentaire ?

Notation	Signification
Δ	variation totale globale
d	variation totale locale
	variation partielle locale
δ	quantité élémentaire