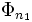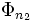Oscillateur harmonique quantique - Définition

Oscillateur anharmonique

Le modèle harmonique d'un puits de potentiel est certes une approche intéressante et finalement assez simple, mais pour étudier les écarts à l'harmonicité d'un système réel, il va falloir pousser le développement limité du potentiel à un ordre supérieur. On introduit alors un terme perturbatif W dans l'hamiltonien puis, à l'aide de la théorie des perturbations stationnaires, on va calculer les nouvelles énergies du système.

Terme en x³

Si l'on pousse le développement limité du potentiel à l'ordre 3, on obtient le terme perturbatif suivant par rapport à l'oscillateur harmonique : où ε est très petit par rapport à 1. Le mouvement de la particule dans un tel potentiel n'est plus tout à fait symétrique. Le calcul théorique des énergies donne alors :

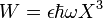
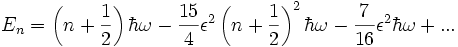
L'utilisation de la méthode des perturbations pour ce calcul impose un résultat approché (correction du deuxième ordre ici). On remarque alors que les niveaux d'énergie ont été abaissés par cette correction. Le calcul des nouvelles fonctions d'onde montre qu'elles sont formées par des couplages entre les anciennes :

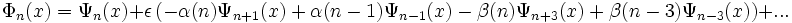
Application

Une molécule diatomique dans le modèle harmonique peut absorber et émettre des ondes électromagnétiques à la pulsation ω. Or dans la pratique, on observe d'autres raies absorbées ou émises : le modèle anharmonique permet de bien en rendre compte, puisque d'après la nouvelle expression des fonctions d'onde, deux états et peuvent etre reliés même si n₁ et n₂ différent de plus de 1. La constante ε peut ainsi être calculée dans cet exemple en analysant le spectre d'absorption.