Pafnouti Tchebychev - Définition
La liste des auteurs de cet article est disponible ici.
La suite de ses travaux par ses élèves
Avant de mourir, Tchebychev a fourni à ses élèves de l’université de Saint-Pétersbourg un enseignement inestimable. Ses élèves, Markov et Liapounov, lui succédèrent et approfondirent ses travaux, lançant ainsi une tradition russe autour des probabilités, ce qui conduira aux travaux de Kolmogorov, le véritable père des probabilités contemporaines. D’autre part, Liapounov établit une théorie de la stabilité et du mouvement des systèmes mécaniques déterminés par un nombre fini de paramètres. Avant lui, les problèmes de stabilité étaient résolus en linéarisant les équations différentielles et en négligeant tout ce qui était d’ordre supérieur. L’avancée significative de Liapounov est d’avoir avancé une méthode générale pour la solution des problèmes de stabilité. Markov, de son côté, étudia la théorie des probabilités en apportant beaucoup à cette branche des mathématiques et mis au point les fameuses chaînes de Markov, il établit une solution simple pour déterminer la limite supérieure de la dérivée d’un polynôme en connaissant la limite supérieure de ce polynôme. D’autres travaux de Tchebychev furent repris à travers l’Occident surtout par les nombreux contacts qu’il s’était faits pendant ses voyages ; comme par exemple la démonstration du postulat de Bertrand qui conduisit Hadamard et de La Vallée-Poussin à mettre à jour le théorème des nombres premiers.
Ses recherches, ses travaux, son œuvre
Dans l’ensemble de son œuvre, Tchebychev s'est penché aussi bien sur les mathématiques fondamentales qu'appliquées. Il a ainsi inventé plusieurs machines à calculer. Il a également étudié la théorie des nombres, démontrant le postulat de Bertrand ou encore les résultats sur la fonction indicatrice d'Euler. Une part importante de ses travaux a concerné les probabilités, et c’est ainsi qu’il reste connu pour les polynômes qui portent son nom. Il les introduisit dans un article sur la mécanique qui reprenait l’ensemble de ses trouvailles à l’issue de sa vie. Nombre de ses articles seront écrits en français et publiés dans le journal de Crelle. À la fin de sa carrière, Tchebychev se voulait mathématicien international plutôt que russe.
Dès le début de ses études, Tchebychev a révélé un sens inné pour la recherche et c’est en tant que professeur-chercheur qu’il va mener sa vie. Ses travaux ont surtout concerné les probabilités et les approximations, et ont débouché sur les polynômes qui portent son nom. Cela va entre autres l’amener à étudier les polynômes orthogonaux. Avec son ami Bienaymé, il va établir une formule qui lui permettra plus tard de démontrer le postulat de Bertrand. Cette formule sera aussi utilisée dans le cadre de travaux sur les théorèmes limites.
Travaux en calcul des probabilités
En ce qui concerne ses travaux en probabilités, Tchebychev posa les bases de l’application de la théorie des probabilités pour les statistiques, en généralisant les théorèmes de Moivre et Laplace dans son ouvrage On two theorems concerning probability. Il généralisera également dans la théorie des intégrales la fonction bêta, et examinera les intégrales de la forme
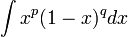
Polynômes de Tchebychev
Définition
Les polynômes de Tchebychev sont définis comme des polynômes d'interpolation et notés généralement Tn. On les utilise dans les approximations polynomiales de fonctions numériques. Ils sont définis sur l'intervalle [ − 1;1] par
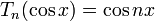
Ainsi, avec n appartenant aux entiers naturels, on appelle polynôme de Tchebychev de degré n l’application définie par :
![T_n : [-1; 1] \rightarrow \R,\qquad T_n(x) = \cos(n\,\arccos(x))](https://static.techno-science.net/illustration/Definitions/autres/8/8bad5650b6b92f9506300544529e7f17_a267928014c54422ff5e6b4d422513b7.png)
Relation de récurrence entre les polynômes de Tchebychev
Énoncé : on a
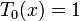
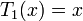
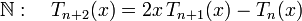
Intérêt
L’interpolation de Lagrange provoque un problème de convergence (due au phénomène de Runge). Tchebychev s’est aperçu qu’en utilisant les racines de ces polynômes comme points d’interpolation, on peut réduire la marge d’erreur provoquée par l’interpolation ; c’est d’ailleurs dans ce but qu’il a étudié ces polynômes. D’autre part, on verra plus loin que les polynômes de Tchebychev sont utilisés en électricité analogique dans le cadre des filtres. Ils sont également utilisés pour démontrer le théorème d'approximation de Weierstrass dont l’énoncé est le suivant : Toute fonction continue sur un intervalle est limite uniforme d'une suite de polynômes.
Inégalité de Bienaymé-Tchebychev
Tchebychev a beaucoup travaillé dans le cadre des probabilités, on le considère d’ailleurs comme celui qui a lancé la théorie des probabilités contemporaine. En 1867, il publia l’article On mean values dans lequel il présentait l’inégalité de Bienaymé-Tchebychev afin de donner une loi générale des grands nombres.
Énoncé : soit X une variable aléatoire réelle d'espérance E(X) = m et de variance V(X) = σ2. Alors,  .
.
Théorèmes limites et conjecture de Gauss
Jacques Bernoulli, Abraham de Moivre et Siméon Denis Poisson avaient déjà travaillé sur les théorèmes limites. Tchebychev reprit leurs travaux, et démontra les tendances asymptotiques des phénomènes naturels. Il établit une loi des grands nombres très générale et donna une nouvelle méthode de démonstration basée sur l'inégalité démontrée par Bienaymé.
Poussant toujours plus loin ses travaux, en 1848, il obtint des résultats sur la conjecture de Gauss (1792). Soit π(n) le nombre de nombres premiers inférieurs à n. Gauss conjecture que la fonction π(n) équivaut à
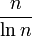
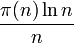
Riemann a lui aussi tenté de démontrer cette conjecture, mais sans succès. Il a étudié les zéros de la fonction zêta, émettant l'hypothèse (hypothèse de Riemann) qu'ils ont tous une partie imaginaire égale à 1/2. Cette hypothèse est le 8e problème de Hilbert et n’est toujours pas démontrée.
Postulat de Bertrand (aussi appelé théorème de Tchebychev)
(Démontré grâce à la formule de Tchebychev)
Énoncé : Pour tout entier n > 2, il existe au moins un nombre premier compris entre les entiers n et 2n.
Histoire : Cette conjecture est énoncée et admise par Joseph Bertrand. Il la vérifie jusqu'à 3 106. Elle ne sera démontrée qu'en 1851 par Tchebychev qui utilise dans sa démonstration l'inégalité qui porte son nom. Le mathématicien allemand Robert Breusch l'améliore en 1931, il démontre que pour tout entier n > 47, il existe un nombre premier entre n et 9n / 8. Le mathématicien hongrois Paul Erdős propose en 1932 une autre démonstration.
Grâce à l’affirmation de la conjecture de Gauss, il réussit à prouver que p(2n) − p(n) > 0 pour tout n > 1, ce qui démontre la conjecture énoncée par Bertrand : Pour tout entier n au moins égal à 2, il existe un nombre premier entre n et 2n.
Édouard Lucas énonce la conjecture de Bertrand sous une autre forme : Pour 2a > 7, il y a au moins un nombre premier compris entre a et (2a − 2). Ceci peut également s'écrire : pour tout entier a > 3, il existe (au moins) un nombre premier p tel que a < p < 2a − 2. Posons a − 1 = n : pour 2n > 5, il y a au moins un nombre premier compris entre n + 1 et 2n, donc compris entre n et 2n. L'inégalité 2n > 5 implique, en nombres entiers, n au moins égal à 3. Mais si n = 2, le nombre 3 est premier entre 2 et 4, d'où la formulation donnée.
Filtres de Tchebychev
En électronique analogique, il existe une famille de filtres nommée filtres de Tchebychev. On les nomme ainsi en raison de leurs caractéristiques mathématiques, qui sont dérivées des polynômes de Tchebychev.
Les filtres de Tchebychev sont un type de filtre caractérisé par l'acceptation d'une ondulation, soit en bande passante, soit en bande atténuée. Dans le cas d’une bande passante, on parle de filtres de Tchebychev directs ou de type 1 ; dans le cas d’une bande atténuée, on parle de filtres de Tchebychev inverses ou de type 2. Les filtres qui présentent une ondulation à la fois en bande passante et en bande atténuée sont appelés filtres elliptiques.
Filtre de type 1 (direct)
Le filtre de Tchebychev de type 1 présente de multiples ondulations en bande passante, mais, à ordre constant, il permet une meilleure sélectivité que le filtre de Butterworth. La valeur maximale des ondulations en bande passante est un paramètre de conception du filtre. Plus cette valeur est importante (à ordre constant), plus le filtre est sélectif (i. e. sa pente est plus raide hors bande passante). Au voisinage de la fréquence de coupure, le déphasage est plus perturbé que pour le filtre de Butterworth, ce qui peut être préjudiciable, notamment en transmission de données (distorsion de phase). Dans les cas où l'ondulation et le déphasage ne posent pas de problème, on retrouve assez couramment ce type de filtre.
Filtre de type 2 (inverse)
Le filtre de Tchebychev de type 2 est le dual du filtre de Tchebychev de type 1. Il présente une évolution monotone en bande passante et des ondulations en bande atténuée. La courbe de réponse oscille entre une série de maximums, avec une valeur spécifiée par le constructeur du filtre, et une série de points où l'atténuation est totale : il s’agit des pôles. À cause de la présence des pôles à des fréquences finies, le filtre de Tchebychev de type 2 présente une configuration de base qui utilise, du point de vue de la réalisation analogique, des composants simples avec des circuits LC série ou parallèle. Toujours en analogique, la nécessité de régler les circuits LC précisément entraîne des complications de conception. Par contre, en numérique, il n'y a pas plus de difficulté de conception qu'avec le type 1, auquel il est alors souvent préféré (à cause de meilleures caractéristiques en bande passante).

















































