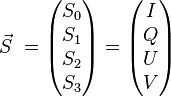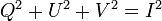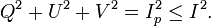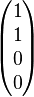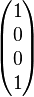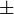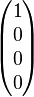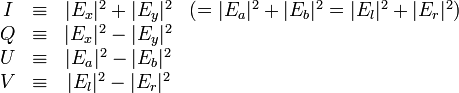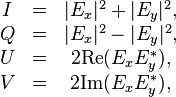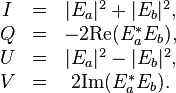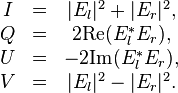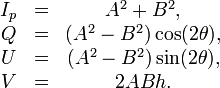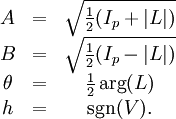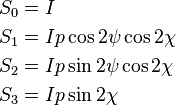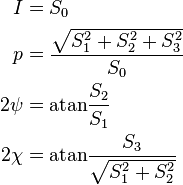Paramètres de Stokes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les paramètres de Stokes sont un ensemble de quatre valeurs qui décrivent l'état de polarisation d'une onde électromagnétique (dont notamment la lumière visible). Ils doivent leur nom à George Gabriel Stokes qui les a introduits en 1852.
Les paramètres sont souvent notés sous forme d'un vecteur, le vecteur de Stokes, et s'expriment en fonction de l'intensité totale du faisceau, son taux de polarisation et des paramètres liées à la forme de l'ellipse de polarisation. Ils permettent de décrire la lumière non polarisée, partiellement polarisée et totalement polarisée. En comparaison, le formalisme de Jones ne permet de décrire que la lumière totalement polarisée. De plus, cette représentation est particulièrement adaptée à l'expérience car chaque paramètre correspond à une somme ou une différence d'intensités facilement mesurables.
L'effet d'un système optique sur la polarisation de la lumière peut être déterminé en construisant le vecteur de Stokes pour la lumière incidente et en utilisant les matrices de Mueller pour obtenir le vecteur de Stokes de la lumière en sortie du système.
Principe
On rassemble habituellement les paramètres de Stokes dans un vecteur, le vecteur de Stokes :
On peut voir les paramètres de Stokes comme trois intensités généralisées.
- I : l'intensité totale mesurée, strictement positive,
- V : l'intensité de polarisation circulaire, qui peut être positive ou négative selon le sens de rotation,
-
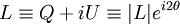
Pour une lumière cohérente et purement monochromatique, on peut montrer que
Pour un faisceau incohérent et partiellement polarisé, les paramètres de Stokes sont définis comme des valeurs moyennes. L'équation précédente devient alors une inégalité :
Le rapport Ip / I est appelé taux de polarisation.
Exemples
On donne ci-dessous quelques vecteurs de Stokes pour des états de polarisation usuels de la lumière.
| Polarisation | Vecteur de Stokes | Polarisation | Vecteur de Stokes |
|---|---|---|---|
| rectiligne horizontale |
| rectiligne verticale |
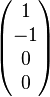
|
| circulaire gauche |
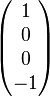
| circulaire droite |
|
| rectiligne à
|

| Lumière non polarisée |
|
Définitions
On peut donner plusieurs définitions des paramètres de Stokes selon la manière dont on décrit l'état de polarisation de la lumière.
Une onde plane monochromatique est caractérisée par son vecteur d'onde

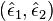
Avec les composantes du champ électrique
Les paramètres de Stokes sont définis en fonction des composantes du champ électrique par
où les indices renvoient à trois bases : la base canonique du repère cartésien (
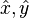
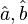
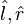
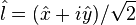
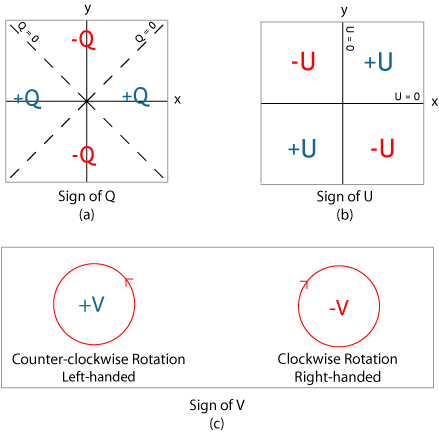
Il est également possible d'exprimer les paramètres de Stokes dans chacune des trois bases seules. Dans la base (
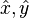
Dans la base
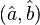
et dans la base
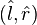
En fonction des paramètres de l'ellipse
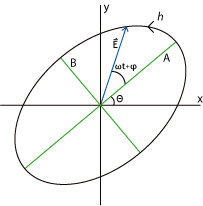
Une façon de décrire la polarisation est de donner le demi grand axe et le demi petit axe de l'ellipse de polarisation, son orientation et le sens de rotation. On passe des paramètres de l'ellipse de polarisation aux paramètres de Stokes à l'aide des expressions suivantes :
et inversement :
En coordonnées sphériques
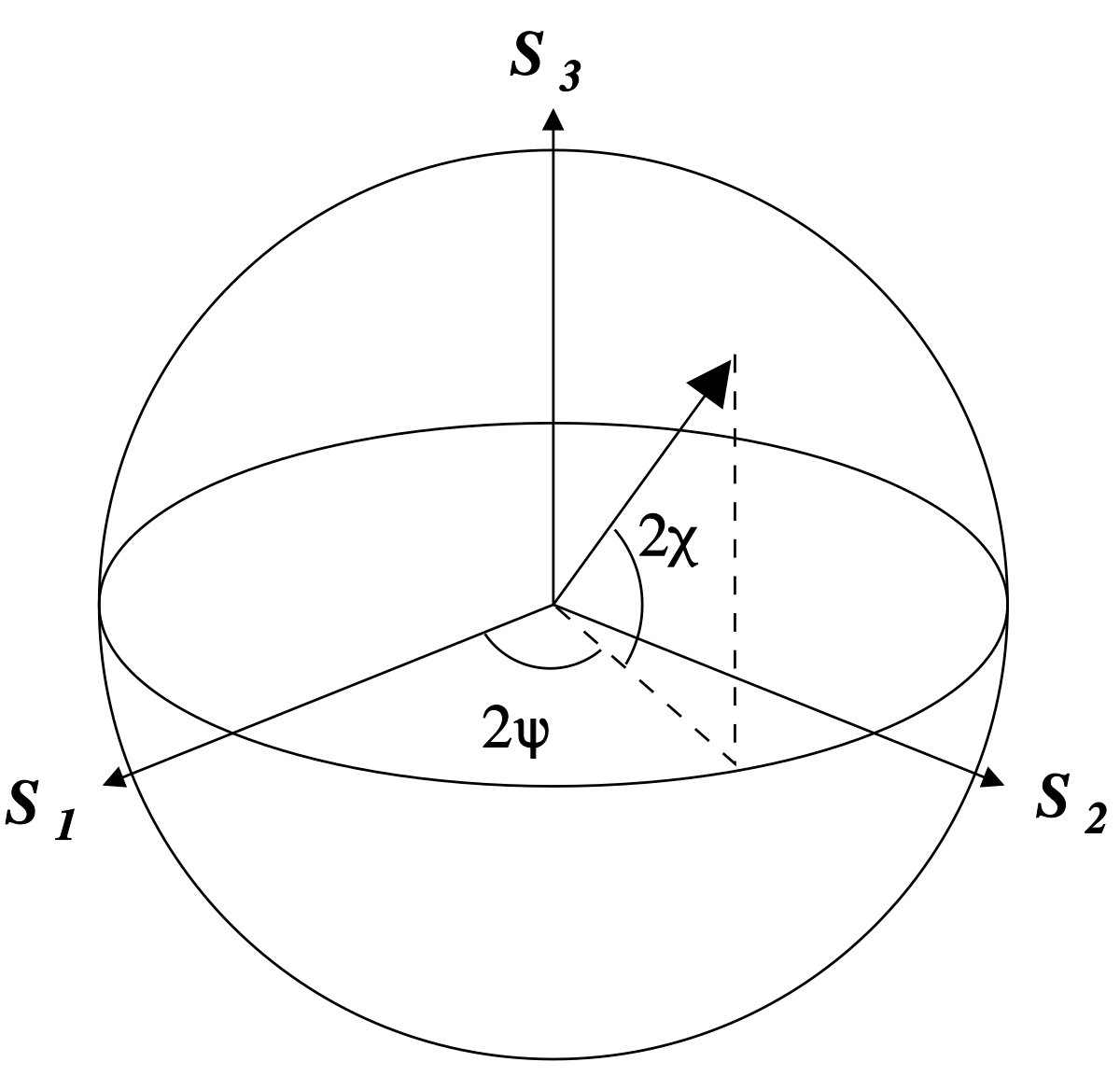
Cette représentation s'appuie sur une paramétrisation différent de l'ellipse.
Ici, Ip, 2ψ et 2χ sont les coordonnées sphériques de l'état de polarisation dans l'espace à trois dimension des trois derniers paramètres de Stokes. Le facteur 2 devant ψ représente le fait qu'une ellipse ne peut pas être distiguée de son image par une rotation de 180 °, tandis que le facteur deux devant χ indique qu'une ellipse ne peut pas être distinguée de son image par une inversion de ses deux axes suivie d'une rotation de 90 °. Les quatre paramètres de Stokes sont parfois notés I, Q, U et V respectivement.
Si on donne les paramètres de Stokes, on peut résoudre le problème inverse et retrouver les coordonnées sphériques grâce aux équations suivantes :