Parité (arithmétique) - Définition

Introduction

En arithmétique modulaire, étudier la parité d'un entier, c'est déterminer si cet entier est ou non un multiple de deux. Un entier multiple de deux est un entier pair, les autres sont les entiers impairs.

Histoire

L'opposition pair/impair apparaît chez Épicharme (vers 490 av. J.-C.) : "Si tu ajoutes un caillou à un nombre impair de cailloux, ou si tu préfères à un nombre pair, ou si tu enlèves l'un de ceux qui sont déjà là, crois-tu que leur nombre va rester le même ? Non, je ne le crois pas" (Diogène Laërce, III, 11).

Euclide dans ses Éléments (Livre VII et Livre IX - propositions 21 et suivantes) étudie les propriétés des nombres pairs et impairs et définit aussi les nombres pairement pairs (double d'un nombre pair), pairement impairs (produit d'un nombre pair et d'un nombre impair), impairement impair (produit de deux nombres impairs) mais exclut de son étude le nombre 1 et le nombre 0.

Arithmétique des nombres pairs et impairs

Les lois suivantes peuvent être vérifiées en utilisant les propriétés de la divisibilité. Elles sont un cas particulier de règles dans l'arithmétique modulaire, et sont communément utilisées pour vérifier si une égalité semble correcte en testant la parité de chaque côté :

Somme et différence

Les règles analogues à celles-ci pour la divisibilité par 9 sont utilisées dans la méthode de preuve par neuf.

• pair ± pair = pair ;
• pair ± impair = impair ;
• impair ± impair = pair.

De manière plus générale, une somme ou différence de plusieurs entiers pairs est toujours paire. Une somme ou différence de plusieurs entiers impairs est

• paire quand le nombre d'entiers qui la compose est pair
• impaire quand le nombre d'entiers de la somme est impair.

Produit

Ces règles sont valables parce que 2 est un nombre premier; les règles analogues pour la divisibilité par un nombre composé seraient plus complexes.

• pair × pair = pair ;
• pair × impair = pair ;
• impair × impair = impair.

Divisibilité et quotient

Un nombre pair ne peut jamais diviser un nombre impair. Un nombre impair peut diviser un nombre pair mais alors, il divise aussi sa moitié.

Le quotient de deux nombres entiers n'est pas nécessairement un nombre entier. Par exemple, 1 divisé par 4 égale 1/4, qui n'est ni pair ni impair, les concepts pair et impair ne s'appliquant que sur les entiers. Mais lorsque le quotient est un entier, c'est-à-dire quand l'un divise l'autre, on peut établir les règles suivantes

• pair / impair = pair ;
• impair / impair = impair ;
• impair / pair n'est jamais un entier ;
• pair / pair peut être pair ou impair.

Exposant

Si a est un réel strictement négatif, alors le signe de aⁿ dépend de la parité de n

• Si n est pair alors aⁿ est positf
• Si n est impair alors aⁿ est négatif

Si P est une fonction polynôme à valeur dans

• Si tous les exposants de x sont pairs, alors, pour tout réel x, P(- x) = P(x)
• Si tous les exposants de x sont impairs, alors, pour tout réel x, P(- x) = - P(x)

On dit que les polynômes du premier type sont pairs et les polynômes du deuxième type sont impairs.

Si P(x) = x⁴ + 7x² - 5, alors P est pair

Si P(x) = x⁵ + 8x³ - 6x, alors P est impair

C'est cette référence à la parité de l'exposant qui a donné leur nom aux fonctions paires et impaires

Nombres pairs et impairs

En mathématiques, tout entier, naturel ou relatif est soit pair soit impair.

• S'il est multiple de deux, c'est un nombre pair. Par exemple, les nombres : -4, 8, et 60, sont pairs. Le nombre zéro est pair, parce qu'il est égal à 2 multiplié par 0.
• Sinon, le nombre est impair. Par exemple -5, 3, et 71 sont impairs. Le nombre un est impair, c'est le plus petit entier naturel impair.

L'ensemble des entiers naturels pairs peut être écrit comme ceci :

Entiers naturels pairs = {0, 2, 4, 6, 8, 10, 12, 14,...} =

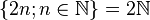
et l'ensemble des entiers relatifs pairs peut s'écrire comme ceci :

Entiers relatifs pairs = {..., - 8, - 6, - 4, - 2, 0, 2, 4, 6, 8, 10, 12, 14,...} =

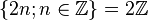
De même, les ensembles des entiers impairs naturels ou relatifs s'écrivent :

Entiers naturels impairs = {1, 3, 5, 7, 9, 11, ...} =

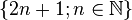
Entiers relatifs impairs = {..., - 9, - 7, - 5 , - 3, - 1, 1, 3, 5, 7, 9, 11, 13,...} =

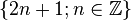
Tout entier naturel pair se décompose de manière unique en produit d'une puissance de deux et d'un entier naturel impair.

18 se décompose en 2 × 9

504 = 8 × 63 = 2³ × 63