Projection cartographique - Définition

Introduction

Le choix d'une projection et la conversion d'une projection à une autre comptent parmi les difficultés que les cartographes ont dû affronter. L'informatique leur a beaucoup apporté de ce point de vue

La projection cartographique est un ensemble de techniques géodésiques permettant de représenter la surface de la Terre dans son ensemble ou en partie sur la surface plane d'une carte.

Description

D'un point de vue mathématique, une projection permet d'établir entre la surface de la Terre et le plan (ou la surface développable) une correspondance telle que :

et

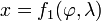
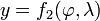
où x,y désignent des coordonnées planes, la latitude, λ la longitude et f₁,f₂ des fonctions qui sont continues partout sur l'ensemble de départ sauf sur un petit nombre de lignes et de points (tels que les pôles). Il existe donc une infinité de solutions. Les mathématiciens ne se sont pas privés d'en trouver, et on en connaît plus de deux cents (Joly, 1985, page 39).

Les types de projections

Une fois un ellipsoïde fixé, on peut choisir le type projection à appliquer pour obtenir une carte. Cette fois encore, ce choix est conduit par l'usage qui sera fait de la carte mais aussi de la position de la région à cartographier sur le globe. Les projections peuvent avoir diverses propriétés :

• projection équivalente : conserve localement les surfaces ;
• projection conforme : conserve localement les angles, donc les formes ;
• projection aphylactique : elle n'est ni conforme ni équivalente, mais peut être équidistante, c'est-à-dire conserver les distances sur les méridiens.

Une projection ne peut pas être à la fois conforme et équivalente.

Une carte ne pouvant pas être obtenue simplement en écrasant une sphère, la projection passe généralement par la représentation de la totalité ou une partie de l'ellipsoïde sur une surface développable, c'est-à-dire une surface qui peut être étalée sans déformation sur un plan.

Les trois formes mathématiques courantes qui répondent à ce critère (à savoir le plan, le cylindre et le cône) donnent lieu aux trois types principaux de projections :

• la projection cylindrique ;
• la projection conique ;
• la projection azimutale.

Une projection qui ne peut être classée dans un de ces types est appelée individuelle ou unique.

Projection cylindrique

On projette l'ellipsoïde sur un cylindre qui l'englobe. Celui-ci peut être tangent au grand cercle, ou sécant en deux cercles. Puis on déroule le cylindre pour obtenir la carte.

Exemples de projection cylindrique :

• Projection de Mercator (conforme)
• Projection de Peters (équivalente)
• Projection de Robinson (pseudo-cylindrique, aphylactique)
• Projection UTM aussi appelée Gauss-Kruger (conforme)
• Projection cylindrique équidistante
• Projection de Mercator oblique (utilisée en Suisse par exemple).

Projection conique

On projette l'ellipsoïde sur un cône tangent à un cercle ou sécant en deux cercles. Puis on déroule le cône pour obtenir la carte.

Exemples de projection conique :

• Projection conique conforme de Lambert
• Projection d'Albers

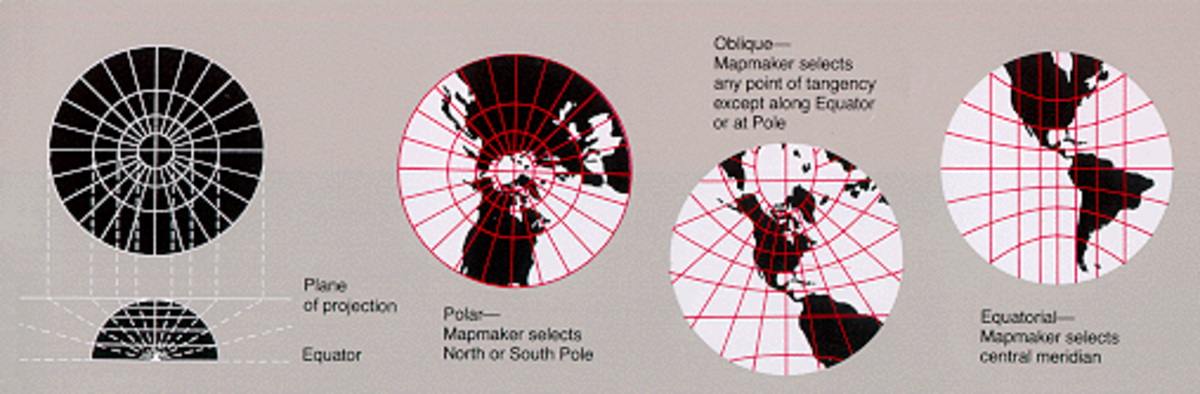
Projection azimutale

On projette l'ellipsoïde sur un plan tangent en un point ou sécant en un cercle.

Il existe trois types de projections azimutales, qui se différencient par la position du point de perspective utilisé pour la projection :

• projection stéréographique ;
• projection gnomonique ;
• projection orthographique.

Par ailleurs, selon la position du plan tangent, la projection azimutale est dite polaire (plan tangent à un pôle), équatoriale (plan tangent en un point de l'équateur), ou oblique (plan tangent en un autre point). La projection azimutale polaire sert pour les cartes représentant les lignes aériennes qui passent par les régions polaires afin de réduire la distance de parcours.

Projection stéréographique

Le point de perspective est placé sur le sphéroïde ou l'ellipsoïde à l'opposé du plan de projection. Le plan de projection, qui sépare les deux hémisphères nord et sud de la sphère, est appelé plan équatorial.

Projection gnomonique

Différentes projections gnomoniques

Le point de perspective est au centre du sphéroïde. La projection gnomonique conserve les orthodromies.

• Projection de Fuller : projection gnomonique sur un polyèdre : cuboctaèdre (14 faces, 8 triangles équilatéraux et 6 carrés) ou plus souvent icosaèdre (20 triangles équilatéraux).

Projection orthographique

Le point de perspective est à une distance infinie. On perçoit un hémisphère du globe comme si on était situé dans l'espace. Les surfaces et formes sont déformées, mais les distances sont préservées sur des lignes parallèles.

Projection azimutale équivalente de Lambert

Projections uniques

Il existe de nombreuses cartes qui ne résultent pas d'une projection sur un cône, un cylindre ou un plan:

• Projection sinusoïdale
• Projection de Sanson-Flamsteed : une projection sinusoïdale découpée et rédressée
• Projection Goode : projection interrompue
• Projection de Winkel-Tripel : mélange entre deux projections