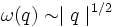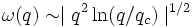Plasmon - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

Dans un métal, un plasmon est une oscillation de plasma quantifiée.
Les oscillations de plasma d'un métal peuvent être comprises dans le cadre d'une théorie classique. Si on suppose que les ions sont fixes, et que les électrons peuvent se déplacer en bloc, et que $x$ est la position du centre de masse des électrons par rapport au centre de masse des ions, lorsque $x\ne 0$ , il existe un excès de charges positives d'un côté du système (supposé de dimension finie dans la direction parallèle à x) et un excès de charge négative du côté opposé. Ces excès de charges constituent une force de rappel qui tend à ramener $x$ à zéro.
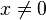
Cependant, s'il n'y a pas de dissipation, l'énergie mécanique totale étant conservée, le centre de masse des électrons va effectuer des oscillations à une pulsation appelée pulsation plasma $ω p$ .
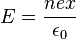
Dans le cas où on suppose que le métal est limité le long de la direction $x$ , et infini dans les directions perpendiculaires, on peut calculer la pulsation plasma en utilisant le théorème de Gauss pour calculer le champ électrique créé par les excès de charge. On trouve que les excès de charges créent un champ électrique : $E=\frac{n e x}{\epsilon_0}$ , où $n$ est la densité d'électrons, ce qui conduit à une pulsation plasma :

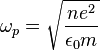
$\omega_p=\sqrt{\frac{n e^2 }{\epsilon_0 m}}$ .

Pour tenir compte du caractère quantique de la dynamique des électrons, on utilise l'approximation de la phase aléatoire et la théorie de la réponse linéaire pour calculer la constante diélectrique $ε(q,ω)$ .
Les oscillations de plasma sont obtenues lorsque le calcul quantique redonne la fréquence classique pour les oscillations de plasma. Il montre aussi qu'il existe des oscillations de plasma pour un vecteur d'onde $q\ne 0$ , avec :

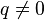
$\omega(q)=\omega_p\left[1+\frac{3}{10}\frac{q^2 v_F^2}{\omega_p^2}\right]$

où $v F$ est la vitesse de Fermi des électrons. Le facteur $3 / 10$ vient de l'approximation de la phase aléatoire. Les approximations plus précises donnent des corrections au facteur devant $q 2$ .

Les oscillations de plasma se comportent comme des particules quantifiées appelées plasmons. Comme les énergies de ces particules sont de l'ordre de $10$ à $20$ eV dans les métaux, il n'existe pas de plasmons dans un métal à l'équilibre. Il est cependant possible d'exciter les modes de plasmons en utilisant des électrons ou des rayons X pour bombarder un film métallique suffisamment fin. Les électrons ou les photons X peuvent céder de l'énergie aux plasmons ce qui permet leur détection.

Jusqu'ici, nous n'avons parlé que du cas tridimensionnel. Il est cependant possible de réaliser des gaz d'électrons bidimensionnels (par exemple avec des interfaces $S i / S i O 2$ ou dans des puits quantiques AlAs/GaAs) ou unidimensionnels (fils quantiques). Dans le cas bidimensionnel, la dispersion des plasmons est de la forme $\omega(q)\sim \mid q\mid^{1/2}$ et dans le cas unidimensionnel de la forme $\omega(q)\sim \mid q ^2 \ln (q/q_c) \mid^{1/2}$ .