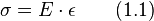Plasticité et endommagement des polymères - Définition

Introduction

Les polymères sont des matériaux complexes dont le comportement face à la pression varie : sous de faibles contraintes, ils réagissent en se déformant de manière élastique et viscoélastique ; sinon, ils suivent un comportement plastique dont il résulte ce qu'on appelle de l'endommagement. Au niveau macroscopique, les phénomènes de déformation plastique se traduisent principalement par l’apparition de bandes de cisaillement et/ou de craquelures.

La plasticité est influencée par divers paramètres que sont principalement la température et la vitesse de sollicitation. Elle n’est pas forcément néfaste pour les polymères, cependant au-delà du seuil de plasticité (défini par les échelles de Tresca ou de Von Mises), l’endommagement nuit aux propriétés mécaniques (rigidité, résistance mécanique) et peut mener à la rupture de la pièce.

Courbe contrainte-déformation

Pour comprendre le comportement d'un matériau polymère lors d'une sollicitation en traction par exemple, et donc prédire sa rupture, les polyméristes s'appuient sur des courbes décrivant l'évolution de la contrainte en fonction de la déformation. Ces courbes, décrivant le comportement mécanique, sont découpées en différents domaines.

Pour des petites déformations, le polymère suit un comportement linéaire décrit par la loi de Hooke :

C'est le domaine élastique.

Pour des déformations légèrement supérieures, on entre dans le domaine viscoélastique.

Le seuil de plasticité, noté y, représente la limite entre le domaine élastique et le domaine plastique. Typiquement, ce seuil intervient aux environs de 5 à 15 % de déformation.

Pour le domaine plastique, on distingue différentes zones :

• l'apparition de la striction, où la déformation plastique est instable du fait de la localisation des déformations. Cette striction est générée par les bandes de cisaillement ;
• la zone d'étirage, qui s'étend sur de grandes déformations et qui correspond à l'allongement et à l'alignement des chaînes de polymère à contrainte constante ;
• le durcissement final, étape durant laquelle les chaînes sont en extension ;
• la rupture, où le polymère cède.

Apparition de la plasticité : seuil et critères de plasticité

La définition de la contrainte de glissement au seuil de plasticité est générale et valable pour la majorité des matériaux. Comme nous l’avons évoqué précédemment, en dehors du domaine élastique, les déformations dues à la présence des plans de glissement deviennent irréversibles.

Pour mieux détailler l’aspect mécanique des déformations, on considérera un essai de traction uniaxial.

La force F, faisant un angle α avec la normale au plan de glissement et un angle θ avec la direction de glissement, alors sa composante dans la direction de glissement est F*cos(θ).

Ainsi, la contrainte exercée sur la surface A du plan, appelée contrainte de cisaillement ou de glissement, ou encore scission s’écrit :

σ =(F/A)*cos(θ)*cos(α) = σ*cos(θ)*cos(α) (3.1)

Seuil de plasticité

Si on augmente la force F à partir de zéro, la déformation plastique du cristal commence à se produire pour une valeur maximale de σc (scission critique de glissement). En général, on peut montrer que le début de la plasticité a lieu lorsque le seuil de plasticité vaut :

σ = 2*σ (3.2)

Certains polymères ne présentent pas de seuil de plasticité σy. C’est le cas des polymères fragiles où l’échantillon casse au stade viscoélastique, ou des élastomères dont le comportement est hyperélastique. Si ce seuil de plasticité σy n’existe pas, on montre que la déformation plastique débute pour des valeurs de l’ordre de 5 à 10 %.

Critères de plasticité généraux

On considère le cas d’une déformation uniaxiale (traction-compression), ce qui permet de définir un seuil de plasticité σy en traction ou compression.

On établit alors un critère de plasticité attaché à une notion de valeur critique, à partir de laquelle se produit une déformation irréversible.

Deux des plus courants critères sont détaillés ici :

• le critère de Tresca ;
• le critère de Von Mises.

Pour simplifier les choses, on choisit les trois axes principaux orthogonaux, tels que les contraintes de cisaillement soient nulles. Le tenseur des contraintes devient :

(3.3)

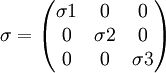
Le critère de Tresca

Le critère de Tresca, établi en 1867, spécifie qu'un matériau va se déformer plastiquement lorsque la contrainte de cisaillement maximale atteint une valeur critique σc. Si les trois contraintes principales sont telles que σ1 >σ2 >σ3 , le critère de Tresca s’écrit :

(σ1-σ3)=2*σc=σy (3.4)

Le critère de Von Mises

Le critère de Von Mises, établi en 1913, prédit que la déformation plastique débute lorsque l’énergie de distorsion atteint une valeur critique ; il peut s’écrire par une relation entre les contraintes principales :

(σ1-σ2)² + (σ2-σ3)² + (σ3-σ1)² = 2*σy² (3.5)

Représentation graphique des critères de Tresca et de Von Mises

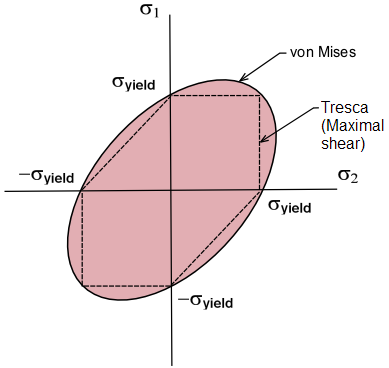
Pour simplifier les calculs des deux critères, on annule la contrainte σ3. Le critère de Von Mises devient donc :

(σ1/σy)² + (σ2/σy)² - (σ1/σy)*(σ2/σy) = 1 (3.6)

Ceci est l’équation d’une ellipse.

De même, le critère de Tresca se traduit par six segments de droites :

• Si σ1>σ2>0 → σ1=σy
• Si σ1>0>σ2 → σ1-σ2=σy
• Si 0>σ1>σ2 → σ2=-σy
• Si σ2>σ1>0 → σ2=σy
• Si σ2>0>σ1 → σ2-σ1=σy
• Si 0>σ2>σ1 → σ1=-σy

On peut ainsi tracer l’ensemble de ces courbes sur un même graphique :

Sur cette figure, on remarque que les deux critères sont très proches et que les deux courbes coïncident pour chaque sommet de l’hexagone de Tresca, c’est-à-dire que les deux critères prédisent un seuil de plasticité identique en traction comme en compression. Ce constat est observé en général pour tous les matériaux hormis pour les polymères car ces derniers sont sensibles à la pression hydrostatique.

Effet de la pression hydrostatique sur le seuil de plasticité

Expérimentalement, on constate pour la plupart des polymères que :

• le seuil de plasticité σy en traction est plus faible que celui en compression uniaxiale. En effet, la contrainte de compression augmente fortement entre les unités constitutives du polymère et donc le glissement va être plus difficile ;

• le seuil de plasticité σy croît fortement avec la pression hydrostatique car les polymères sont sensibles à la pression, du fait de l’existence du volume libre disponible entre les unités constitutives.

Les critères de Von Mises et de Tresca ne tenant pas compte de ces deux effets, nous allons désormais les modifier pour prendre en compte l’influence de pression sur le seuil de plasticité.

Critère de Tresca modifié

Pour rendre compte de l’effet hydrostatique dans le critère de Tresca, la valeur critique σc devient une fonction linéaire de la pression hydrostatique, notée P :

σc=σc0 - µ*P (3.7)

où :

• µ est le coefficient de frottement dépendant du matériau. En général pour les polymères, ce coefficient µ est positif ;
• σc0 est la valeur de σc lorsque aucune pression n’est appliquée ;
• P est la moyenne des trois contraintes principales : P=(σ1+σ2+σ3)/3.

Remarquons que P en tension est positif et P en compression est négatif.

Cette formule indique que la valeur critique σyc augmente en compression (la pression P étant négative en compression), et σyt diminue en tension (pression positive). La plasticité en compression est donc plus difficile qu’en traction.

Critère de Von Mises modifié

De même que le critère de Tresca, le critère de Von Mises peut se transformer en introduisant la pression hydrostatique P. P étant toujours défini comme la moyenne des trois contraintes principales. Pour la plupart des polymères solides, le critère de Von Mises modifié se formule par :

A*(σ1+σ2+σ3)+ B*((σ1-σ2)² + (σ2-σ3)² + (σ3-σ1)²)=1 (3.8)

où A et B sont deux constantes dépendant de la pression hydrostatique.

On peut déterminer A et B en mesurant les seuils de plasticité en traction uniaxiale σyc et en compression uniaxiale σyt, car dans ces deux cas σ1=σy et σ2=σ3=0.

Ainsi, le critère de Von Mises prend la forme suivante :

2*(σyc-σyt)*(σ1+σ2+σ3)+(σ1-σ2)² + (σ2-σ3)² + (σ3-σ1)² = 2*σyc*σyt (3.9)

Représentation graphique des critères de Tresca et Von Mises modifiés

Graphiquement, le critère de Von Mises modifié s'apparente à une ellipse déformée au sein de laquelle s'inscrit toujours le critère de Tresca.

Les critères classiques prédisaient un seuil de plasticité identique en traction ou en compression, or il s’avère que les critères modifiés imposent un seuil de plasticité supérieur en compression qu’en traction.

Par analogie avec les critères de plasticité de Tresca et Von Mises, on peut établir un critère d’endommagement par craquelures étant donné que les craquelures apparaissent au-delà d’une déformation critique fonction de la pression hydrostatique. On peut ensuite relier cette déformation à la contrainte par la loi de Hooke (1.1). On montre alors que :

σ1-ν*σ2 ≥ C + D/(σ1+σ2) (3.10)

avec ν le coefficient de Poisson et C et D deux constantes fonction du temps et de la température.

La représentation graphique subit par conséquent une modification.