Potentiel vecteur du champ magnétique - Définition

Introduction

Le potentiel vecteur du champ magnétique, ou, plus simplement potentiel vecteur quand il n'y a pas de confusion possible, est une quantité physique assimilable à un vecteur intervenant en électromagnétisme. Elle n'est pas directement mesurable, mais sa présence est intimement liée à celle d'un champ électrique et/ou d'un champ magnétique.

Formule fondamentale

Le potentiel vecteur du champ magnétique est d'ordinaire introduit en conséquence des équations de Maxwell, qui stipulent que le champ magnétique B est de divergence nulle. L'analyse vectorielle indique qu'un champ vectoriel tridimensionnel de divergence nulle peut toujours s'exprimer sous la forme d'un rotationnel d'un champ de vecteur, noté A. On a ainsi

.

Par ailleurs, l'équation de Maxwell-Faraday relie les variations temporelles du champ magnétique aux variations spatiales du champ électrique (ce qui est à l'origine du phénomène d'induction électromagnétique) selon la formule

,

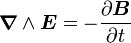
dont on déduit que

.

L'analyse vectorielle indique alors que le champ électrique peut s'exprimer sous la forme de la somme de l'opposé de la dérivée temporelle du potentiel vecteur et d'un terme de rotationnel nul, terme que l'on peut exprimer sous la forme d'un gradient d'une quantité appelé dans ce contexte potentiel électrique et notée V :

.

À noter qu'au départ la relation entre A et B est une relation purement locale. Le problème de savoir si on peut définir globalement un potentiel-vecteur sur un espace donné conduit à devoir se poser des questions sur la cohomologie de cet espace, un concept issu de la géométrie différentielle.

Quelques jauges

Malgré l'indétermination intrinsèque du potentiel vecteur, il est souvent commode de l'utiliser pour résoudre les équations de l'électromagnétisme. Dans ce cas, il faut imposer (de façon artificielle) une contrainte supplémentaire sur le potentiel vecteur pour en sélectionner une configuration parmi les solutions physiquement équivalentes qui sont possible. On parle dans ce cas d'un choix de jauge. On définit ainsi :

• la jauge de Lorenz, par

   ;

• la jauge de Coulomb, par

  .

Même dans ce cas, les jauges ne sont pas toujours définies de façon univoque. Ainsi, la jauge de Coulomb admet-elle plusieurs configuration, car si A obéit pour le problème considéré à la contrainte de la jauge de Coulomb, alors il en est de même pour A' défini par

si la fonction ϕ obéit à la contrainte supplémentaire

Δφ = 0,

ou Δ est l'opérateur laplacien. De même, la jauge de Lorenz est définie à une ambiguité près sur ϕ si celui-ci obéit à la contrainte supplémentaire

,

où représente le d'alembertien.

Potentiel vecteur et invariance de jauge

Le potentiel vecteur et le potentiel électrique sont des entités plus fondamentales que les champs électrique et magnétique, mais ne sont pas définis de façon univoque. En effet, le rotationnel d'un gradient étant nul, on peut toujours ajouter un gradient à un potentiel vecteur A pour que celui-ci génère un même champ magnétique B. Une fois ceci fait, on obtient le même champ électrique en redéfinissant le potentiel électrique : si l'on modifie le potentiel vecteur A en

,

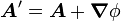
alors le champ électrique E est donné par

,

c'est-à-dire que l'on a

,

avec

,

.

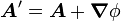
Cette propriété d'indétermination du potentiel vecteur (et du potentiel électrique) est intimement liée à celle, plus intuitive de la conservation de la charge électrique et résulte d'une propriété mathématique générale appelée invariance de jauge.