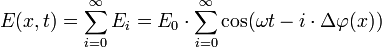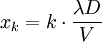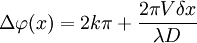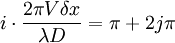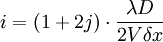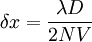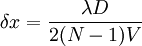Réseau de diffraction optique - Définition

Introduction

Un disque compact agit comme un réseau de diffraction : on observe des irisations colorées.

Un réseau de diffraction est un dispositif optique composé d'une série de fentes parallèles (réseau en transmission), ou de rayures réfléchissantes (réseau en réflexion). Ces traits sont espacés de manière régulière, l'espacement est appelé le « pas » du réseau.

Si la distance entre les traits est de l'ordre de grandeur de la longueur d'onde de la lumière, le réseau permet d'obtenir des figures de diffraction :

• si l'on envoie de la lumière blanche, le réseau décompose la lumière un peu à la manière d'un prisme ; c'est le phénomène qui se produit sur les disques compacts, la lumière est diffractée par les variations qui forment les bits et qui jouent le rôle des traits du réseau ;
• si l'on envoie une seule longueur d'onde (lumière monochromatique), le réseau réfléchit plusieurs taches ; la direction de réflexion des taches dépend de la distance entre les traits et de la longueur d'onde.

Formules d'optique

Le principe des réseaux de diffraction repose sur une même formule pouvant être démontrée soit par l'optique géométrique, soit par la théorie électromagnétique de Maxwell. Il se base sur le principe de Huygens-Fresnel.

Le calcul sur un réseau est très similaire au calcul fait sur les fentes de Young (voir cet article) : la différence de marche entre deux traits (donc le déphasage des rayons diffusés par deux traits voisins) se calcule de la même manière. La différence est qu'au lieu d'avoir la somme de deux fonctions d'onde, on a la somme d'une série « infinie » (le nombre de traits étant très grand) :

en reprenant les notations de l'article Fentes de Young :

• x est l'abscisse du point sur l'écran de visualisation, sur un axe perpendiculaire aux traits du réseau ;
• est l'amplitude de l'onde incidente arrivant sur le trait 0, ω étant la pulsation ;
• est le déphasage entre deux traits voisins, avec
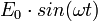
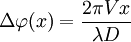
  • V le pas du réseau ;
  • D la distance entre le réseau et l'écran de visualisation de la figure de diffraction (écran parallèle au plan du réseau).

Si l'on est en condition de diffraction entre deux traits (cas des fentes de Young), on l'est également entre tous les traits : le déphasage est partout un multiple de 2π. On va donc avoir de maxima d'intensité en

ou bien, si l'écran est « à l'infini » (c'est-à-dire à plusieurs mètre ou bien dans le plan focal image d'une lentille convergente), on considère l'angle de déviation α donnant un maximum d'intensité :

Largeur des raies et taille du réseau

La différence entre un réseau et des fentes de Young est que l'intensité va s'annuler dès que l'on s'écarte des conditions de diffraction. Au lieu d'avoir un pic dont la forme est en cos², on a un pic très fin : si l'on se place en x_k + δx, alors

un trait i sera en opposition de phase avec le trait 0 s'il existe un entier j vérifiant

soit :

Dans le cas des fentes de Young, il n'y a annulation que lorsque λD/2Vδx est entier ; ici, il suffit de prendre j suffisamment grand pour que la fraction devienne entière. En théorie (nombre infini de traits éclairés), l'intensité est donc nulle hors condition de diffraction (l'ensemble des réels est l'adhérence de l'ensemble des rationnels).

Dans la pratique, le réseau a un nombre fini de traits, et seule une portion du réseau est éclairée. Si l'on appelle N le nombre de traits éclairés, alors l'intensité s'annule pour la première fois lorsque

si N est impair, ou en

s'il est pair. La largeur du pic est donc divisée par N (ou N-1) par rapport aux fentes de Young.

Le cas de la diffraction à l'infini peut se traiter dans l'espace réciproque.