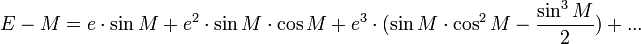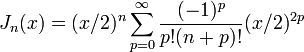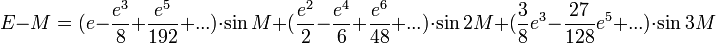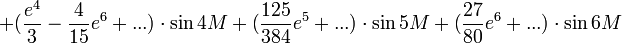Résolution de l'équation de Kepler - Définition
La liste des auteurs de cet article est disponible ici.
Série entière de l'excentricité
C'est encore Lagrange qui trouve la solution ; et Laplace donnera le rayon de convergence. Ces travaux inspireront Cauchy, qui fondra la théorie des séries analytiques pour résoudre ce problème épineux, celui-ci verra son aboutissement avec les travaux de Puiseux.
L'application du théorème d'inversion de série de Lagrange fournit:
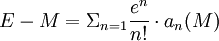
avec
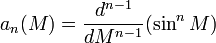
- Le rayon de convergence minimum de la série, qui dépend de M, est atteint pour M= π/2, et vaut: eo = 0.6627434193
tel qu'indiqué par Laplace (1823) et démontré par Cauchy et Puiseux :
- et x tel que
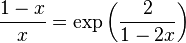
Ceci rend cette formule inapplicable pour déterminer la position des comètes, dont l'excentricité est souvent voisine de 1.
Les premiers termes sont :
Note: il est possible d'obtenir ce développement en série en remplaçant dans la série de Fourier précédente les fonctions de Bessel par leur développement limité :
On obtient alors le développement limité beaucoup plus simplement que par la méthode de l'inversion de série :
Il est à noter que bien que la série de Fourier converge pour 0 Le premier à se confronter au problème est Horrocks, puis surtout Halley (1705), pour les calculs sur sa comète d'excentricité e = 0,9673. Une généralisation de l'équation de Barker est un développement en série convergeant d'autant plus rapidement que l'excentricité e est proche de 1, ce qui s'avère bien adapté aux cas des comètes (cette série s'applique aussi aux orbites légèrement hyperboliques): rayon de convergence:
avec S = tan(v / 2) v étant l'anomalie vraie, k la constante gravitationnelle de gauss, e et q étant respectivement l'excentricité et le périastre de l'orbite, t le temps et t0 étant l'instant du passage au périastre. Lorsque e =1, la série se réduit à l'équation de Barker Avant Kepler, l'équation était déjà étudiée pour d'autres motifs : c'est le problème de la réduction des coordonnées locales aux cordonnées géocentriques : il faut réduire la correction de parallaxe. Habash al Hasib s'y est déjà attaqué. Avant 1700, il y a déjà beaucoup de tentatives : Kepler naturellement, Curtz (1626), Niele, Boulliau (1645, 1657), Seth Ward (1653), Paganus (1657), Horrebow (1717), Cassini (1669), Newton (1665?), Wren (1658), Wallis (1659), Jeremiah Horrocks (1638)... Les calculs via les intégrateur symplectiques exigent de rester toujours en butée du nombre de digits, dans le moindre coût de calcul. Bien sûr, cela dépend beaucoup du doublet (M,e), M compris entre 0 et π et de e, surtout quand e est voisin de 1. Nijenhuis (1991) adopte la méthode de Mikkola (1987) qui est la méthode de Newton d'ordre 4, en choisissant « adéquatement » le germe Eo en fonction du doublet (M,e). Il est clair que dans les calculs numériques, le volume de calculs est essentiel, autant que le nombre de décimales, vu l'instabilité du système solaire évaluée à un coefficient de Liapunov de 10^(t/5Myr). On se heurte à une muraille exponentielle : difficile d'aller plus loin que 25 Myr, même avec un traitement 128 bits. Ce sont ces calculs (astronomiques... mais informatisés) qui tournent sur les machines de l'IMCCE-Paris. Le calcul de l'ensoleillement terrestre à la latitude 65°Nord, I(65,t) est calculé et on essaie d'en déduire la corrélation avec le climat passé : l'échelle géologique jusqu'au Néogène (25M ans) en est déduite (échelle géologique Gradstein 2004). Prochaine étape prévue : les 65 M ans. Cas des comètes :

Plusieurs solutions ont été proposés en modifiant légèrement la solution de Barker (e = 1). La solution proposée par Bessel (1805) couvre le domaine e > 0.997. Gauss (1809) s'illustra en donnant une belle solution pour 0,2 < e < 0,95
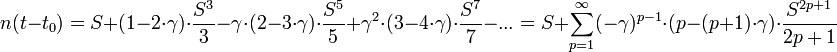
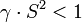
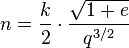
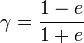
Histoire des sciences
Recherches actuelles
Depuis 300 ans, on cherche la « meilleure » méthode. Elle reste à trouver !