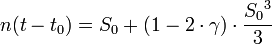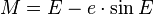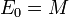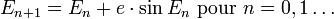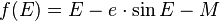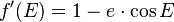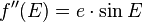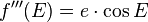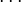Résolution de l'équation de Kepler - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans le mouvement keplerien, l'équation de Kepler relie l'anomalie moyenne M = nt à l'anomalie excentrique E par l'équation
où e est l'excentricité de la planète.
Résoudre cette équation, c'est trouver E(e,M) :
- comme série de Fourier puisque c'est une fonction périodique impaire de M
- comme série de puissance de e, si e < eo := 0.6627..., rayon de convergence de la série.
- comme une valeur numérique avec un nombre de chiffres (d), pour un temps de calcul tc(d) optimisé.
Série de Fourier
C'est Lagrange qui trouve l'expression, bien que le nom Jn(x) soit associé au nom de Bessel.
- E-M = fonction impaire périodique de M :
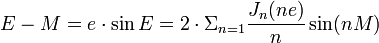
Jn(x) est la fonction de Bessel de 1ere espèce d'ordre n.
E-M est une fonction continue, impaire et périodique de période 2π, donc est développable en série de Fourier, dont les coefficients des cosinus sont tous nuls.
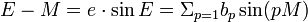
avec
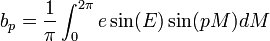
Pour changer la variable d'intégration, on intègre par partie, en posant u=sin(E) et dv=sin(pM).dM, on obtient:
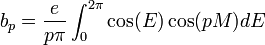
En transformant le produit de cosinus en somme de cosinus, on obtient:
![b_p= \frac{e}{p} ( \frac{1}{2 \pi} \int_{0}^{2 \pi} \cos[(1+p)E-ep\sin(E)]dE + \frac{1}{2 \pi} \int_{0}^{2 \pi} \cos[(1-p)E+ep\sin(E)]dE )](https://static.techno-science.net/illustration/Definitions/autres/7/7c0082e0837cc26b6bf1c7d43628f2eb_8b1fb5df29289f31c3ba133752e4597d.png)
Or, les fonctions de Bessel de première espèce s'expriment par:
![J_p(x)= \frac{1}{2 \pi} \int_{0}^{2 \pi} \cos[pE-x \sin(E)]dE](https://static.techno-science.net/illustration/Definitions/autres/9/97c503261bbe320736139c5f67ddd5e7_9b53cc58c2e81c6d5879f2d466b1398a.png)
d'où:
![b_p= \frac{e}{p}[J_{p+1}(pe)+J_{p-1}(pe)]](https://static.techno-science.net/illustration/Definitions/autres/0/06e5477d61722cc00a140749cabdbf7c_db0ba2326ea7663cfdd429fdd1bb95ec.png)
Par ailleurs, les fonctions de Bessel vérifient la relation de récurrence:
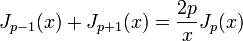
d'où finalement:
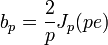
Calcul numérique
L'équation de Kepler peut être résolue à l'aide d'un Algorithme de recherche d'un zéro d'une fonction. Les méthodes du type encadrement, Méthode de dichotomie , Méthode de la fausse position nécessitent un encadrement de départ dans lequel la racine est présente. Du fait de la périodicité et la parité de l'équation de Kepler, il est toujours possible de ramener l'intervalle de départ à [0; π]. Ceci fournit un encadrement de départ pour ces méthode, mais il est aisé d'en trouver de plus fins.
Les méthodes du type point fixe nécessitent une estimation de départ de la racine, le germe de la méthode E0, pour lancer les calculs : il en existe de multiples dans la littérature, dont la plus simple est E0=M.
La méthode de type point fixe la plus simple, celle utilisée par Kepler, est :
converge lentement lorsque e est proche de 1. Il est alors avantageux de lui adjoindre un algorithme d'accélération de la convergence :le Delta-2 de Aitken, par exemple, ou la variante de Steffensen.
L'équation de Kepler se prête particulièrement bien aux algorithmes nécessitant le calcul des dérivées successives élevés, du fait du faible coût en calcul machine nécessaire. En effet :
Les dérivées suivantes se déduisant cycliquement des précédentes. Les variantes de la Méthode de Newton et de Halley d'ordre plus élevés sont donc très performantes dans ce cas. Il est à noter que ces méthodes peuvent dans certains cas avoir des difficultés à converger (e proche de 1 et M proche de 0). Il est préférable dans ces zones soit de proposer une valeur de départ moins grossière (germe de Mikkola), soit de brider les méthodes itératives pour les forcer à converger (modification de Hamming de la méthode de Newton), ou d'utiliser des méthodes itératives à convergence moins locale (Méthode de Laguerre).
Dans le cas des comètes, la résolution de la généralisation quasi-parabolique de l'équation de Barker pose deux problèmes :
- le calcul approché de la série qui peut nécessiter un grand nombre de termes, voire être impossible si elle diverge. Il se trouve que cette série se prête particulièrement bien à l'utilisation d'algorithmes d'accélération de la convergence, notamment l'algorithme ε de Peter Wynn, qui non seulement accélère la convergence, mais étend son domaine de convergence. En pratique, les difficultés interviennent lorsque la comète est très loin de son périastre (elle est alors depuis longtemps invisible), ou son excentricité diffère notablement de 1 (dans ce cas,il est plus judicieux de résoudre l'équation de Kepler elliptique ou hyperbolique).
- La résolution de l'équation proprement dite. Celle-ci peut être effectuée par les méthodes de type Newton avec :
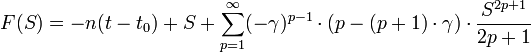
en remarquant que la dérivée s'exprime simplement:
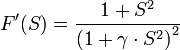
On pourra choisir comme valeur initiale de l'itération S0, la solution de l'équation cubique obtenue en retenant les premiers termes (différant légèrement de l'équation de Barker), à l'aide de la Méthode de Cardan