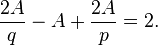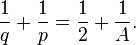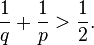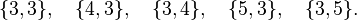Solide de Platon - Définition

Classification

C'est un résultat classique qu'il existe seulement cinq polyèdres réguliers convexes. Deux arguments communs sont donnés ci-dessous. Les deux montrent seulement qu'il ne peut pas y avoir plus de cinq solides de Platon. Que chacun des cinq existe réellement est une question séparée — à laquelle on peut répondre par une construction explicite.

Démonstration géométrique

L'argument géométrique suivant est très similaire à celui donné par Euclide dans les Éléments :

1. Chaque sommet du solide doit coïncider avec un sommet sur au moins trois faces, sinon ce n'est qu'un point de côté et non un sommet.
2. À chaque sommet du solide, le total des angles entre les côtés adjacents relatifs aux faces adjacentes, doit être strictement inférieur à 360°.
3. Les angles de tous les sommets de toutes les faces d'un solide de Platon sont identiques, donc chaque sommet de chaque face doit contribuer pour strictement moins de 360°/3=120°.
4. Les polygones réguliers de six côtés ou plus ont seulement des angles de 120° ou plus, donc la face commune doit être le triangle, le carré ou le pentagone. Et pour :
   • les faces triangulaires : chaque sommet d'un triangle régulier a un angle de 60°, donc une forme doit avoir 3, 4 ou 5 triangles se rencontrant à un sommet ; celles-ci sont le tétraèdre, l'octaèdre et l'icosaèdre respectivement.
   • les faces carrées : chaque sommet d'un carré a un angle de 90°, donc il existe seulement un arrangement possible avec trois faces à un sommet, le cube.
   • les faces pentagonales : chaque sommet a un angle de 108° ; de nouveau, seulement un arrangement, de trois faces à un sommet est possible, le dodécaèdre.

Démonstration topologique

Une démonstration purement topologique peut être donnée en utilisant seulement les informations combinatoires sur les solides. La clé est l'observation d'Euler que S − A + F = 2, et le fait que pF = 2A = qS. En combinant ces équations, on obtient l'équation

Une simple manipulation algébrique donne alors

Puisque A est strictement positif, nous devons avoir

En utilisant le fait que p et q doivent, tous deux, être au moins égaux à 3, on peut facilement voir qu'il existe seulement cinq possibilités pour {p, q} :

En nature et en technologie

Le tétraèdre, le cube et l'octaèdre apparaissent tous naturellement dans les structures cristallines. Ceux-ci épuisent nullement les nombres de formes possibles de cristaux. Néanmoins, ni l'icosaèdre régulier, ni le dodécaèdre régulier ne figurent parmi eux. Une de ces formes, appelée le pyritoèdre (nommé en rapport avec le groupe des minéraux avec lequel il est typique) a douze faces pentagonales, arrangées avec le même motif que les faces du dodécaèdre régulier. Néanmoins, les faces du pyritoèdre ne sont pas régulières, donc, le pyritoèdre n'est pas non plus régulier.

Circogonia icosahedra, une espèce de radiolaire, formée comme un icosaèdre régulier.

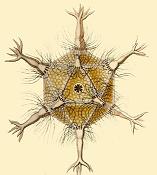
Au début du XX^e siècle, Ernst Haeckel décrivit (Haeckel, 1904) de nombreuses d'espèces de Radiolaires, certaines comportant des squelettes ayant la forme de divers polyèdres réguliers. Ses exemples incluent Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus et Circorrhegma dodecahedra. Les formes de ces crétures étant évidentes d'après leurs noms.

Beaucoup de virus, tel que le virus de l'herpès, ont la forme d'un icosaèdre régulier. Les structures virales sont construites sur des sous-utités de protéines identiques répétées et l'icosaèdre est la forme la plus facile pour assembler en utilisant ces sous-unités. Un polyèdre régulier est utilisé car il peut être construit à partir d'une unité de protéine basique utilisée indéfiniment, ceci engendre un espace dans le génome viral.

En météorologie et en climatologie, les modèles numériques globaux des flux atmosphériques sont d'un intérêt croissant. Ils emploient des grilles qui sont basées sur un icosaèdre (raffiné par triangulation) à la place de la grille longitude/latitude plus communément utilisée. Ceci a l'avantage d'avoir une résolution spatiale également distribuée sans singularités (i.e. les pôles géographiques) aux dépens d'une certaine difficulté numérique plus grande.

La géométrie des armatures d'espace est souvent basée sur les solides de Platon. Dans le système MERO, les solides de Platon sont utilisés pour la convention de nomenclature des diverses configurations d'armatures d'espace. Par exemple ½O+T fait référence à une configuration faite d'un demi-octaèdre et un tétraèdre.

Les solides de Platon sont souvent utilisés pour fabriquer des dés. Les dés à 6 faces sont très communs, mais les autres nombres sont communément utilisés dans les jeux de rôle. De tels dés sont souvent appelés dn où n est le nombre de faces (d8, d20, etc.);

.

Les dés polyèdriques sont souvent utilisés dans les jeux de rôle.

Ces formes apparaissent fréquemment dans d'autres jeux ou d'autres puzzles. Des puzzles similaires aux Rubik's Cube ont vu le jour dans toutes ces formes — voir polyèdres magiques.