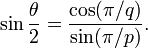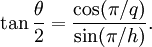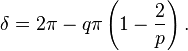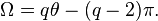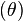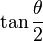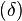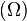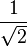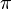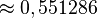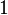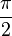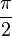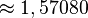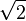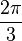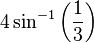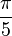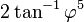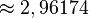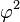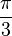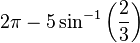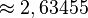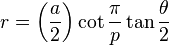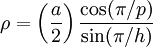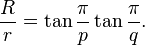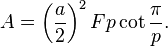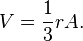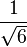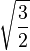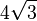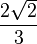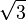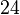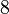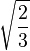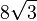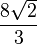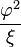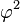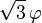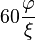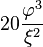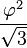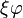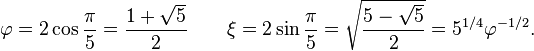Solide de Platon - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés géométriques
Angles
Il existe un nombre d'angles associés avec chaque solide de Platon. L'angle diédral est l'angle interne entre deux faces planes quelconques. L'angle diédral, θ, du solide {p,q} est donné par la formule
Ceci est quelquefois exprimé de manière plus pratique en termes de tangente par
La quantité h est 4, 6, 6, 10 et 10 pour le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre respectivement.
La déficience angulaire au sommet d'un polyèdre est la différence entre la somme des angles d'une face et 2π. La déficience, δ, à un sommet quelconque des sommets de Platons {p,q} est
Par le théorème de Descartes, ceci est égal à 4π divisé par le nombre de sommets (i.e. la déficience totale de tous les sommets est 4π).
L'analogue tridimensionnel d'un angle plan est un angle solide. L'angle solide, Ω, au sommet d'un solide de Platon est donné en termes d'angle diédral par
Ceci provient de la formule de l'excès sphérique pour un polygone sphérique et le fait que la figure de sommet du polyèdre {p,q} est un q-gone régulier.
Les divers angles associés avec les solides de Platon sont donnés ci-dessous. Les valeurs numériques des angles solides sont données en stéradians. La constante
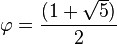
| Polyèdre | Angle diédral |
| Déficience
| Angle solide
| ||
|---|---|---|---|---|---|---|
| Tétraèdre | 70,53° |
|
|
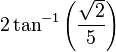
|
| |
| Cube | 90° |
|
|
|
| |
| Octaèdre | 109,47° |
|
|
|
| |
| Dodécaèdre | 116,56° |
|
|
|
| |
| Icosaèdre | 138,19° |
|
|
|
| |
Rayons, aires et volumes
Une autre vertu de la régularité est que les solides de Platon possèdent tous trois sphères concentriques :
- la sphère circonscrite qui passe à travers tous les sommets,
- la sphère moyenne qui est tangente à chaque arête au milieu de celle-ci et
- la sphère inscrite qui est tangente à chaque face au centre de celle-ci.
Les rayons de ces sphères sont appelés les rayons circonscrits, les rayons moyens et les rayons internes. Ceux-ci sont les distances à partir du centre du polyèdre aux sommets, aux milieux des arêtes et aux centres de faces respectivement. Le rayon circonscrit R et le rayon interne r du solide {p, q} avec une longueur d'arête a sont donnés par
où θ est l'angle dièdre. Le rayon moyen ρ est donné par
où h est la quantité utilisée ci-dessus dans la définition de l'angle dièdre (h = 4, 6, 6, 10 ou 10). Noter que le rapport du rayon circonscrit au rayons interne est symétrique dans p et q :
La superficie A d'un solide de Platon {p, q} est facilement calculée, c'est l'aire d'un p-gone régulier fois le nombre de faces F. C’est-à-dire :
Le volume est calculé comme étant F fois le volume de la pyramide dont la base est un p-gone régulier et dont la hauteur est le rayon interne r. C’est-à-dire :
Le tableau suivant liste les divers rayons des solides de Platon ainsi que leurs surfaces et leurs volumes. La taille globale est fixée en prenant la longueur d'arête, a, égale à 2.
| Polyèdre | r | ρ | R | A | V |
|---|---|---|---|---|---|
| Tétraèdre |
|
|
|
|
|
| Cube |
|
|
|
|
|
| Octaèdre |
|
|
|
|
|
| Dodécaèdre |
|
|
|
|
|
| Icosaèdre |
|
|
|
|
|
Les constantes φ et ξ ci-dessus sont données par
Parmi les solides de Platon, le dodécaèdre ou l'icosaèdre peuvent être regardés comme la meilleure approximation de la sphère. L'icosaèdre a le plus grand nombre de face, le plus grand angle dièdre, et son enveloppe est la plus proche de sa sphère inscrite. Le dodécaèdre, d'un autre côté, a la plus petite déflexion angulaire, le plus grand angle solide au sommet et il remplit le plus sa sphère circonscrite.