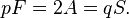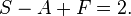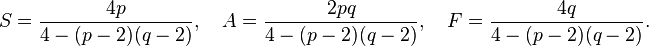Solide de Platon - Définition

Propriétés combinatoires

Un polyèdre convexe est un solide de Platon si et seulement si

1. Toutes ses faces sont des polygones réguliers convexes isométriques — superposables —,
2. Aucune de ses faces ne se coupe, excepté sur les arêtes
3. Le même nombre de faces se rencontrent à chacun de ses sommets.

Chaque solide de Platon peut par conséquent être noté par un symbole {p, q} où

p = le nombre de côtés de chaque face (ou le nombre de sommet sur chaque face) et

q = le nombre de faces se rencontrant à chaque sommet (ou le nombre d'arêtes se rencontrant à chaque sommet).

Le symbole {p, q}, appelé le symbole de Schläfli, donne une description combinatoire du polyèdre. Les symboles de Schläfli des cinq solides de Platon sont donnés dans la table ci-dessous.

Polyèdre		Sommets	Arêtes	Faces	Symbole de Schläfli	Configuration de sommet
Tétraèdre		4	6	4	{3, 3}	3.3.3
Hexaèdre		8	12	6	{4, 3}	4.4.4
Octaèdre		6	12	8	{3, 4}	3.3.3.3
Dodécaèdre		20	30	12	{5, 3}	5.5.5
Icosaèdre		12	30	20	{3, 5}	3.3.3.3.3

Toutes les autres informations combinatoires à propos de ces solides, telles que le nombre total de sommets (S), des arêtes (A) et des faces (F) peuvent être déterminées à partir de p et q. Puisque toute arête joint deux sommets et possède deux faces adjacentes, nous devons avoir :

L'autre relation entre ces valeurs est donnée par la formule d'Euler :

Ce fait non-trivial peut être démontré d'une grande variété de manières (en topologie algébrique il découle de ce fait que la caractéristique d'Euler de la sphère est 2). Mises ensemble, ces trois relations déterminent complètement S, A et F :

Note : échanger p et q intervertit F et S laissant A inchangé (pour une interprétation géométrique de ce fait, voir la section sur les polyèdres duaux ci-dessous).

Descriptions et sections planes classiques

Octaèdre et cube

Épure n° 1. Vue en élévation et vue de dessus d’un octaèdre régulier posé sur sa face horizontale KMN.

Épure n° 2. Vue en élévation du même octaèdre régulier.  Il contient son dual :  un cube dont les huit sommets sont les centres des faces de l’octaèdre.

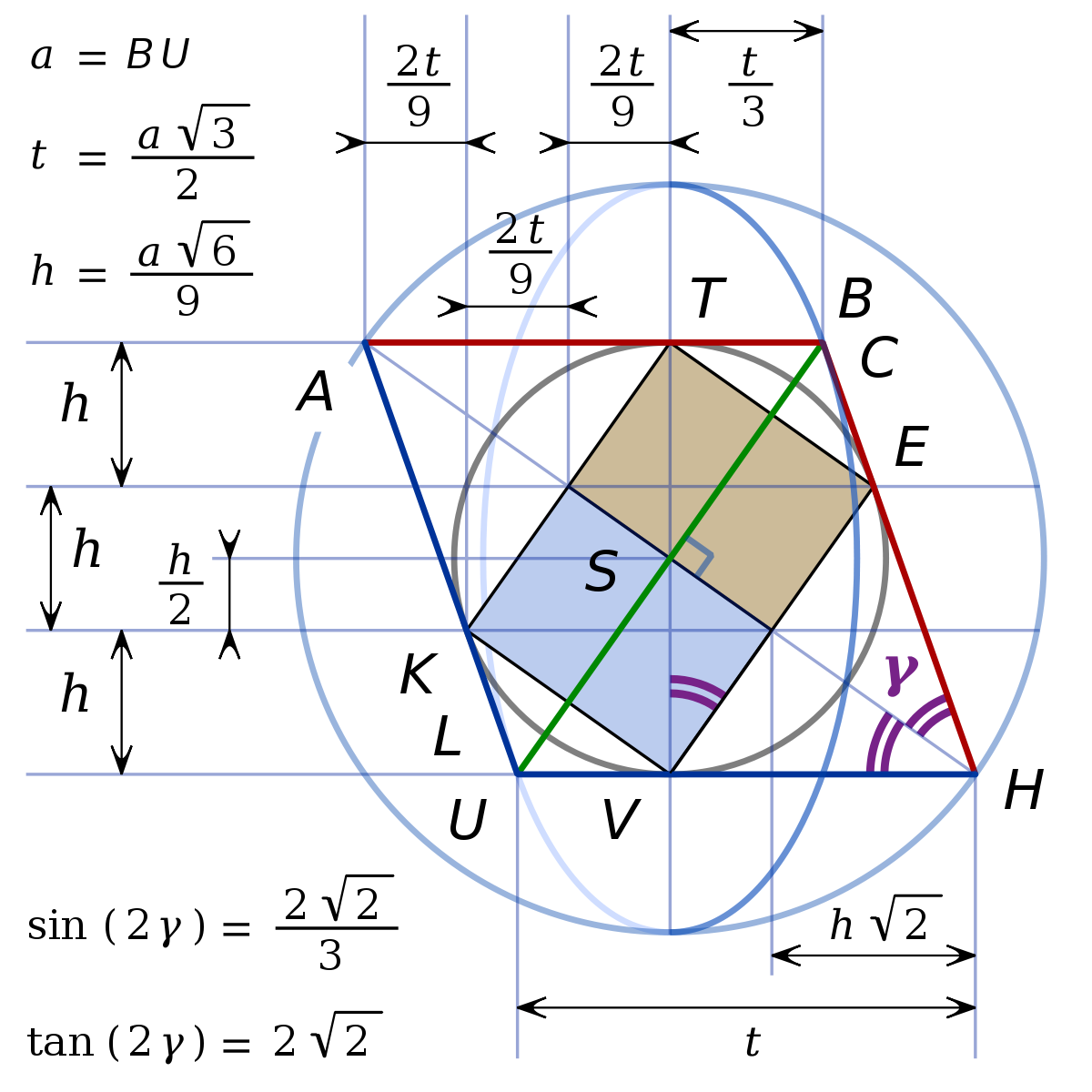
Les huit faces d’un octaèdre régulier sont des triangles équilatéraux.  Pour qu’un polyèdre soit un octaèdre régulier,  il faut et il suffit que ses arêtes soient les côtés de trois carrés,  dont chaque paire a une diagonale commune.  L’épure n° 1 montre les côtés des trois carrés en trois couleurs différentes.  Par exemple,  les carrés ABKM  et BCMN  ont en commun leur diagonale [BM].

Le centre S des trois carrés est le centre de la sphère circonscrite à l’octaèdre.  Les diagonales des carrés en sont trois diamètres.  En élévation,  la perspective n’altère pas la longueur AK,  longueur d’un diamètre de la sphère.  L’épure n° 2 représente la sphère par deux grands cercles verticaux,  dans la même vue en élévation du même octaèdre,  en laissant vides les faces et le volume de l’octaèdre.  Ainsi elle montre mieux un “dual” de l’octaèdre — un cube —,  qui a ses sommets aux centres des faces de l’octaèdre.  Une “diagonale” de ce cube est donc verticale,  autrement dit un segment qui joint deux sommets “opposés” du cube — deux sommets diamétralement opposés sur la sphère circonscrite au cube —.  Nous imaginons la sphère circonscrite au cube grâce au grand cercle vertical tracé en noir.  Cette sphère circonscrite au cube est aussi la sphère inscrite dans l’octaèdre — tangente à ses huit faces —.

Le centre S des trois carrés est aussi le centre de l’hexagone régulier horizontal tracé en blanc,  dont les sommets sont les milieux des six arêtes obliques de l’octaèdre.

Comme l’épure n° 1,  l’épure n° 2 désigne par γ  l’angle entre un plan horizontal et une “diagonale” de l’octaèdre :  l’inclinaison d’une des diagonales des carrés.  Le complément de γ  est l’inclinaison des six arêtes obliques,  ou celle des trois carrés.  Le double de γ  est l’inclinaison d’une face oblique de l’octaèdre régulier.

Dans la vue de dessus,  le contour de l’octaèdre est un hexagone régulier,  parce que l’image de S  est à la fois le centre des deux triangles équilatéraux,  images des deux faces horizontales,  et le centre de la symétrie qui transforme un triangle équilatéral en l’autre.  En élévation,  le contour du solide est un losange.

Plan diagonal de l’octaèdre régulier,  le plan d’un carré partage l’octaèdre en deux pyramides régulières carrées,  symétriques l’une de l’autre par rapport au plan diagonal,  le plan de leur base commune.  Plan diagonal du cube,  un plan qui contient deux arêtes opposées du cube partage le cube en deux prismes symétriques l’un de l’autre par rapport au plan diagonal.  Les plans diagonaux d’un cube sont au nombre de six.  La droite d’intersection de deux d’entre eux est soit une diagonale du cube,  soit la médiatrice commune des diagonales de deux faces opposées du cube.

La perspective de l’épure n° 2 donne au cube un contour semblable à une “section diagonale” du cube,  obtenue en coupant le cube par l’un des ses plans diagonaux.  Ce contour est semblable aussi à l’image d’une face du cube,  semblable encore au format de papier A4,  ou à un format normalisé semblable A5,  A3,  A2,  etc.  En chantier,  l’épure n° 3  montrera des sections diagonales d’un cube.

Cube et tétraèdre

Épure n° 4. Vue en élévation et vue de dessus d’un cube tronqué, posé sur sa face horizontale KMN.  Trois troncatures de plus,  et on obtient le tétraèdre régulier TKMN.

Épure n° 5 en chantier

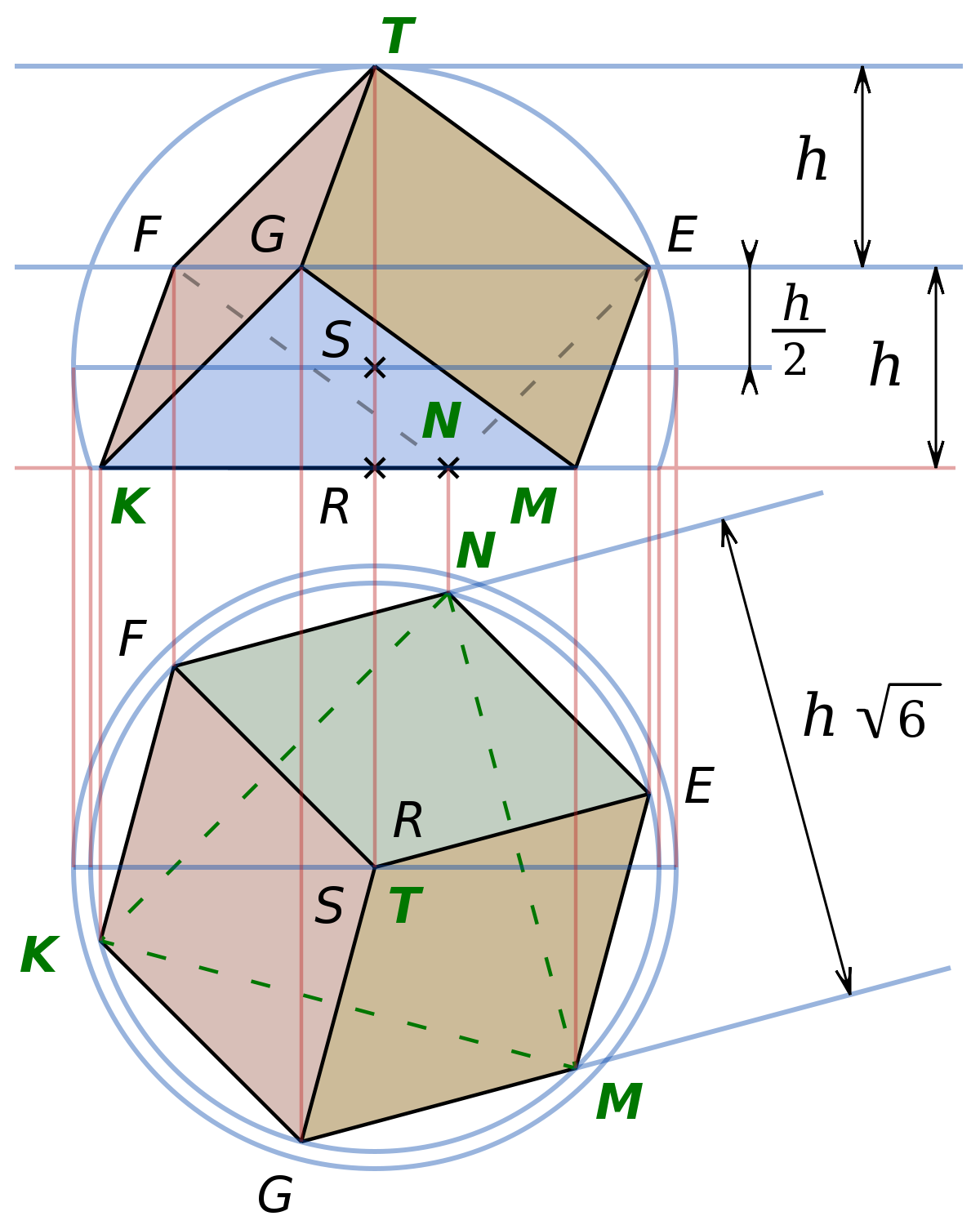
Les six faces d’un cube sont des carrés.  Les deux vues ci-contre donnent deux images d’un même solide posé sur le sol : un cube tronqué.  Le plan de la section triangulaire KMN  contient les diagonales de trois faces du cube.  Le solide est posé sur KMN,  tracé en pointillé dans la vue de dessus :  un triangle équilatéral non altéré par la perspective cavalière.  Comme dans les épures n° 1 et n° 2,  une diagonale du cube est verticale :  le sommet T est à la verticale du centre S de la sphère circonscrite.  L’image des trois faces carrées vues de dessus est un pavage d’hexagone régulier,  comme dans de nombreux logos où figure un cube.  Pourquoi un hexagone régulier ?  Neuf arêtes du polyèdre forment neuf angles égaux avec le plan horizontal de la projection.  Et les neuf arêtes sont égales.  Alors les neuf images des arêtes obliques sont des segments égaux.  La vue en élévation note h  la dénivellation entre les extrêmités d’une arête oblique.

Par quatre troncatures identiques du cube — trois de plus —,  on obtient le tétraèdre régulier TKMN,  qui a une hauteur 2h. L’épure n° 3  ne représente que la face KMN  du tétraèdre TKMN.

Si le solide était à l’intérieur de sa sphère circonscrite,  de centre S,  une règle de géométrie descriptive voudrait que toutes les arêtes soient en pointillé.  Disons que la sphère est absente.  Mais on l’imagine grâce à des lignes bleues de sa surface :  un équateur horizontal,  un arc d’un autre grand cercle, qui passe par le sommet supérieur T,   ou le cercle au sol de centre R,   circonscrit à KMN.

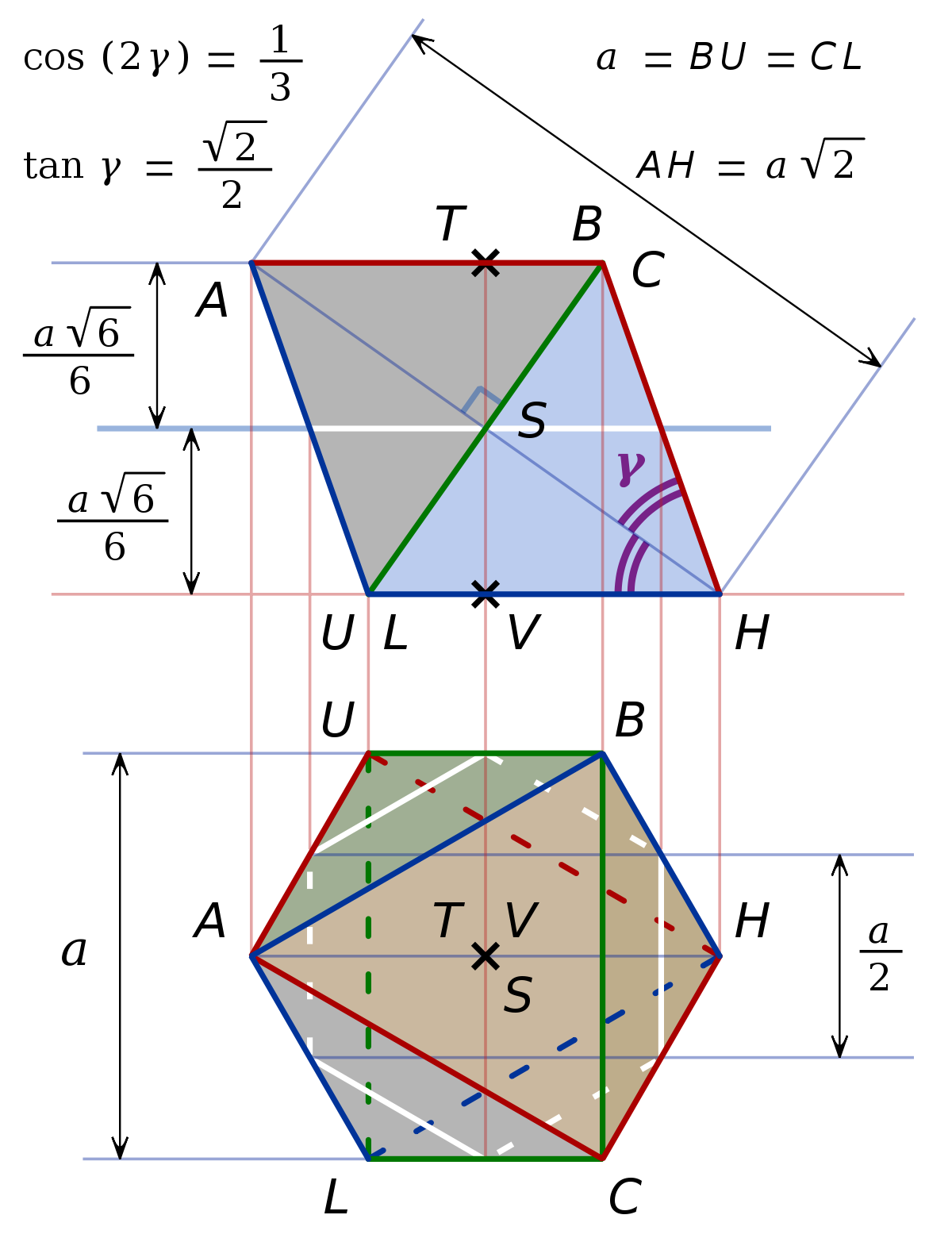
Le plan horizontal qui passe par S  coupe en son milieu chaque arête oblique qui part du sol.  Cette nouvelle façon de tronquer un cube est présentée dans l’épure n° 5 — à paraître —,  où la face au sol du nouveau solide est un hexagone régulier.

Dodécaèdre de Platon

Épure n° 6. Six faces dépliées,  ou moitié d’un patron d’un dodécaèdre de Platon.  Et la perspective esquissée de l’objet obtenu par pliage.

Épure n° 7. Vue en élévation et vue de dessus d’un dodécaèdre de Platon.

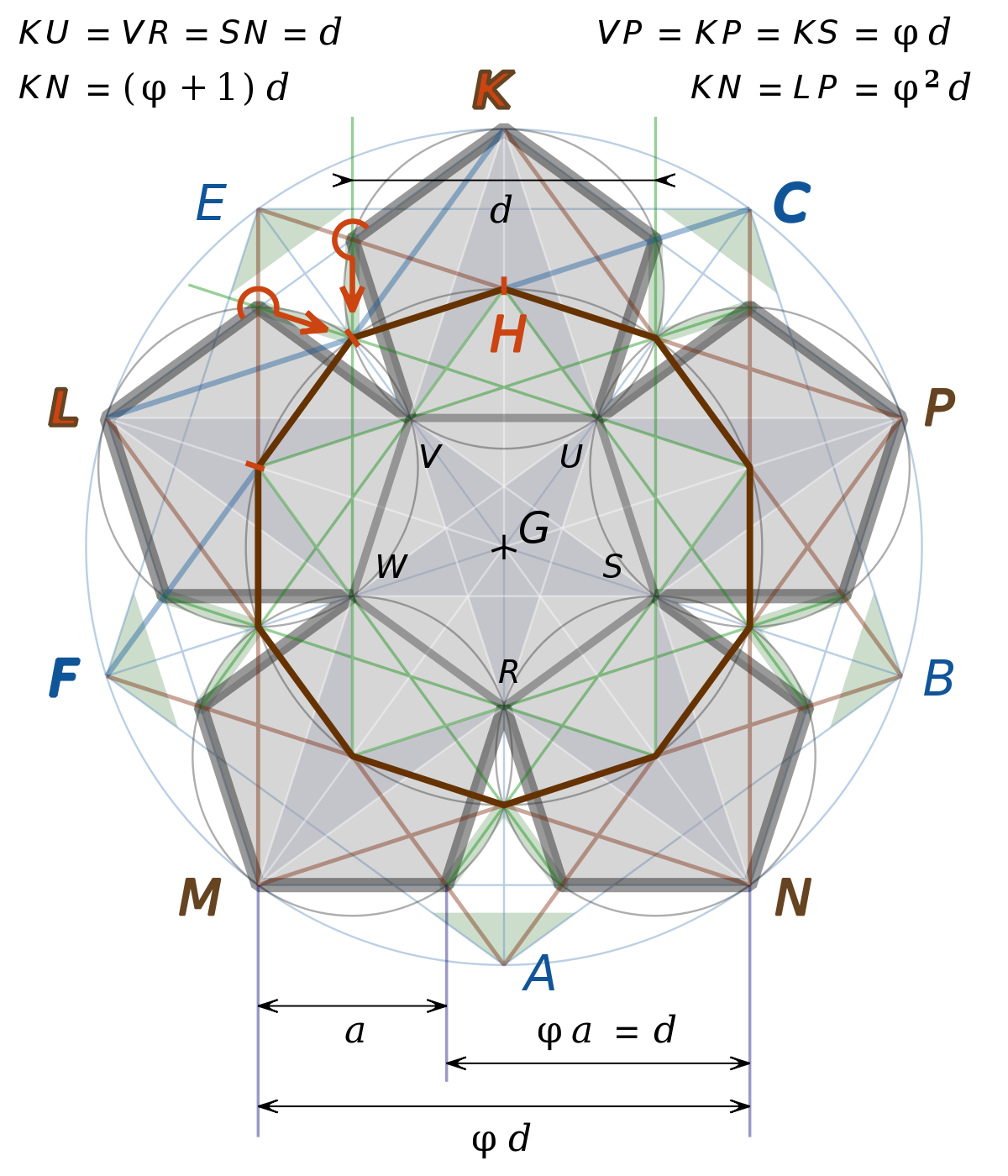
Les douze faces d’un dodécaèdre de Platon sont des pentagones réguliers convexes.  Quand le plan (KUV) tourne autour de la droite fixe (UV) dans le mouvement du pliage,   K  se déplace dans le plan médiateur du segment [UV].  Les deux autres sommets mobiles de cette face se déplacent aussi dans des plans perpendiculaires à l’axe de rotation (UV).   Quand la droite (KL) tourne autour de (UL), son point L  est fixe sur l’axe de rotation :  (KL) devient (HL) dans la perspective,  et K  devient H  dans l’esquisse de la vasque de six faces obtenue par pliage,  ou dans la perspective des faces visibles du dodécaèdre régulier.

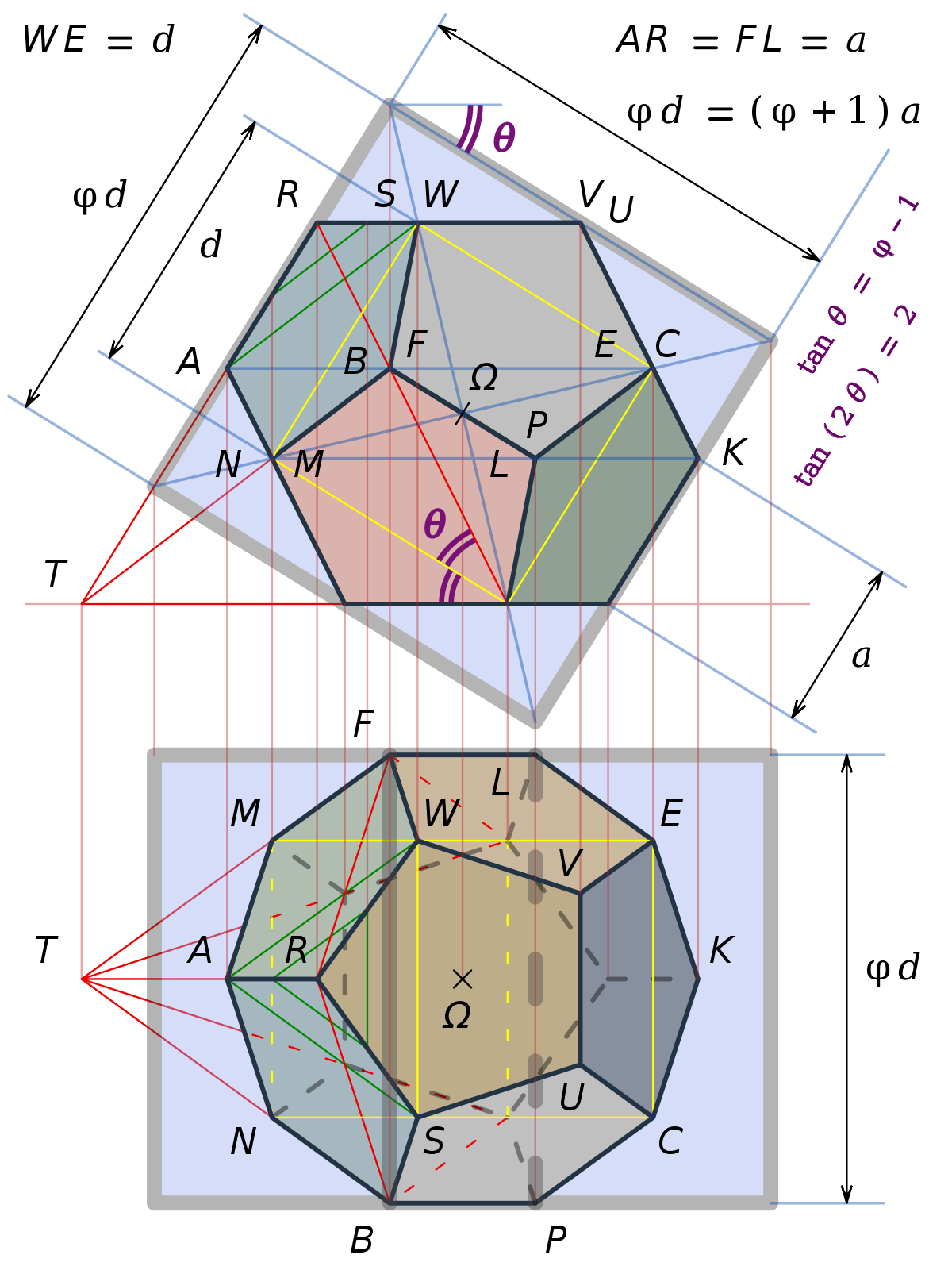
Il n’y a plus de patron dans l’épure n° 7,  le contour de l’objet se voit mieux :  un décagone régulier convexe.  Les deux pentagones réguliers convexes ABCEF  et KLMNP  sont dans deux plans horizontaux distincts.  En transformant par l’homothétie de rapport φ  — le nombre d'or — et de centre T  la face qui contient [MN],  on obtient une section pentagonale isométrique à ABCEF  — superposable à ABCEF —.

Des diagonales de trois faces du solide forment la section triangulaire ASW :  un triangle équilatéral dont les côtés mesurent d,  la longueur d’une diagonale d’une face.  Le segment [SW] tracé en blanc est le seul côté de ASW  dont les perspectives n’altèrent pas la longueur.  Les côtés de six sections carrées sont tracés en blanc :  les six faces d’un cube.  Une seule face du cube a ses côtés visibles en élévation,  où ils forment un vrai carré de dimension d.  Dans la vue en élévation,  θ  est l’angle avec un plan horizontal de deux faces du cube,  ou l’inclinaison des dix arêtes du dodécaèdre qui sont communes à deux faces obliques.  En indiquant des angles adjacents de mesure θ,  des arcs de cercles montrent l’inclinaison 2θ  d’une face pentagonale avec un plan horizontal.

Icosaèdre de Platon