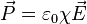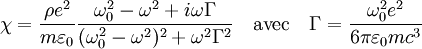Susceptibilité électrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En électromagnétisme, la susceptibilité électrique
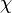
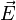
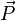
où
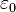
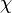
-
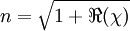
où
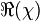
Calcul de la susceptibilité électrique
Pour calculer la susceptibilité électrique, plusieurs approches sont possibles. Il faut dans tous les cas être capable de décrire l'effet d'un champ électrique sur les constituants la matière. Les différents mécanismes possibles sont à l'origine de plusieurs types de polarisation :
- la polarisation électronique, toujours présente, due au déplacement et à la déformation du nuage électronique,
- la polarisation atomique ou ionique due aux déplacements des atomes ou des ions dans la structure du matériau,
- la polarisation d'orientation, pour les matériaux qui sont initialement déjà polarisés de façon microscopique, mais dont les éléments n'ont pas forcément la même orientation,
- la polarisation macroscopique due à des déplacements de charges dans l'ensemble du matériau.
Difficultés du calcul
Dans la plupart des cas, plusieurs de ces phénomènes sont présents et se cumulent. La principale difficulté du calcul réside dans le fait que le champ électrique macroscopique dans lequel est plongé le matériau est souvent différent du champ électrique local qui agit réellement sur les constituants microscopiques et donc crée la polarisation. C'est pourquoi il faut distinguer susceptibilité (grandeur macroscopique) de polarisabilité (grandeur microscopique). Enfin, la polarisation modifiant en retour le champ électrique, il est souvent nécessaire de faire appel à une méthode auto-cohérente.
Exemple : modèle de l'électron élastiquement lié
On se place dans le cas d'un gaz très peu dense soumis à un rayonnement de fréquence ω. La modélisation la plus simple fait appel à la notion d'atome de Lorentz décrivant l'interaction entre un atome et du rayonnement par la mécanique classique. Ce modèle, également appelé modèle de l'électron élastiquement lié, consiste à supposer que les électrons gravitant autour du noyau atomique sont soumis à trois forces :
- la force attractive de la part de ce noyau (supposée correspondre à un oscillateur harmonique de fréquence ω0),
- la force sinusoïdale due au champ électrique
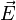
- et une force de freinage en
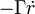
Le mouvement obtenu peut alors être relié à celui d'un dipôle électrique, et finalement, la somme de tous les dipôles est égale à la polarisation
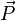
où
- e et m sont la charge et la masse de l'électron,
- ρ est la densité volumique du gaz,
- Γ est une fréquence caractéristique de la force de freinage,
- et c est la vitesse de la lumière dans le vide.