Théorème d'uniformisation - Définition

Introduction

En mathématiques, et plus précisément en géométrie, le théorème d'uniformisation de Poincaré affirme que toute surface admet une métrique riemannienne de courbure constante. On peut en voir comme un cas particulier le théorème d'uniformisation de Riemann, affirmant que toute surface de Riemann simplement connexe est en bijection conforme avec le plan, la sphère ou le disque unité, et comme une généralisation la conjecture de géométrisation de Thurston, démontrée en 2004 par Grigori Perelman.

Le théorème d'uniformisation de Poincaré

Sous sa forme la plus générale, le théorème d'uniformisation de Poincaré affirme que toute surface peut être ramenée à une surface de courbure constante, ou, plus précisément, que :

Ce résultat fut progressivement obtenu par les travaux de Felix Klein vers 1880, puis ceux de Paul Koebe et Henri Poincaré vers 1900, avant que Poincaré n'en donne une démonstration générale en 1907, dans son article sur l'uniformisation des fonctions analytiques ; c'est pourquoi le théorème est parfois connu sous le nom de théorème d'uniformisation de Klein-Poincaré.

Classification des surfaces de Riemann

Le théorème d'uniformisation de Riemann

Passant à l'étude des surfaces de Riemann, il est possible d'en déduire une classification complète : en effet, sur une surface orientée donnée , une métrique riemannienne induit naturellement une structure de variété presque complexe de la manière suivante : si v est un vecteur tangent, on définit J(v) comme le vecteur de même norme, orthogonal à v, et tel que la base (v, J(v)) du plan tangent soit orientée positivement. Comme toute structure presque complexe sur une surface est intégrable, cela transforme la surface orientée en une surface de Riemann. Ainsi, la classification précédente est équivalente à une classification des surfaces de Riemann  : toute surface de Riemann est quotient de son recouvrement universel par l'action libre, propre et holomorphe d'un sous groupe discret, et ce recouvrement universel est lui-même conformément équivalent à l'un des trois domaines canoniques suivants :

1. la sphère de Riemann
2. le plan complexe
3. le disque unité ouvert du plan complexe.

Ceci permet de classer toutes les surfaces de Riemann comme elliptiques, paraboliques ou hyperboliques selon que leur revêtement universel est (respectivement) la sphère, le plan, ou le disque unité.

En particulier, on en déduit le théorème d'uniformisation de Riemann (historiquement obtenu indépendamment, à partir du théorème de l'application conforme) :

Exemples

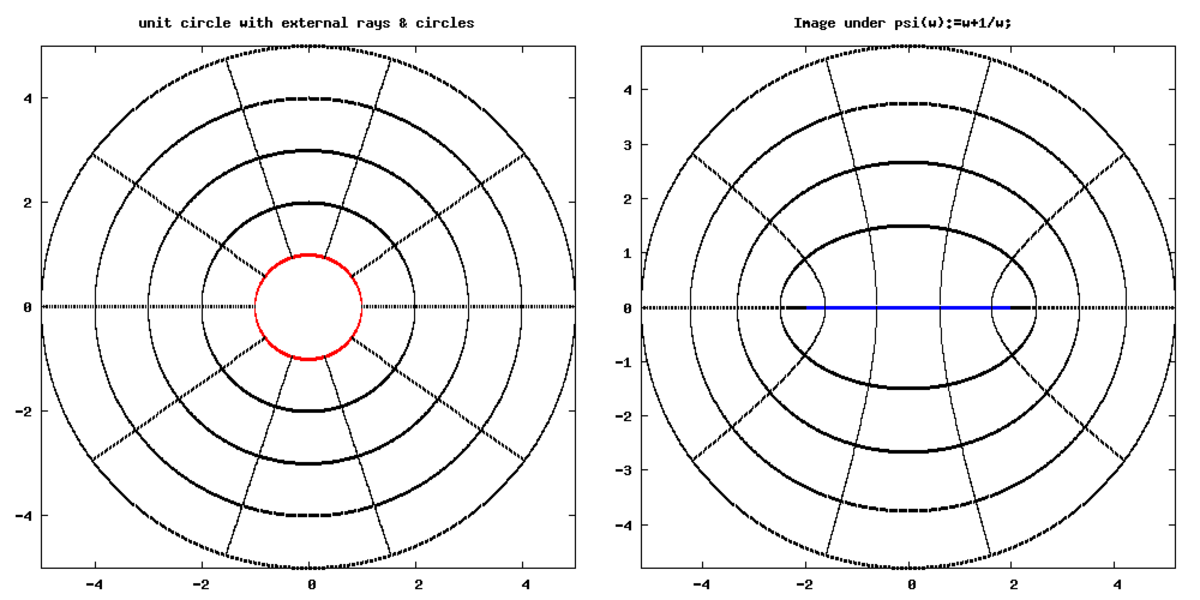
Les graphes ci-dessous correspondent à des uniformisations des complémentaires de l'ensemble de Mandelbrot et du segment [ − 2,2] (ensemble de Julia correspondant à P(x) = x² − 2).

Uniformisation du complémentaire de l'ensemble de Mandelbrot

Uniformisation du complémentaire du segment [ − 2,2]

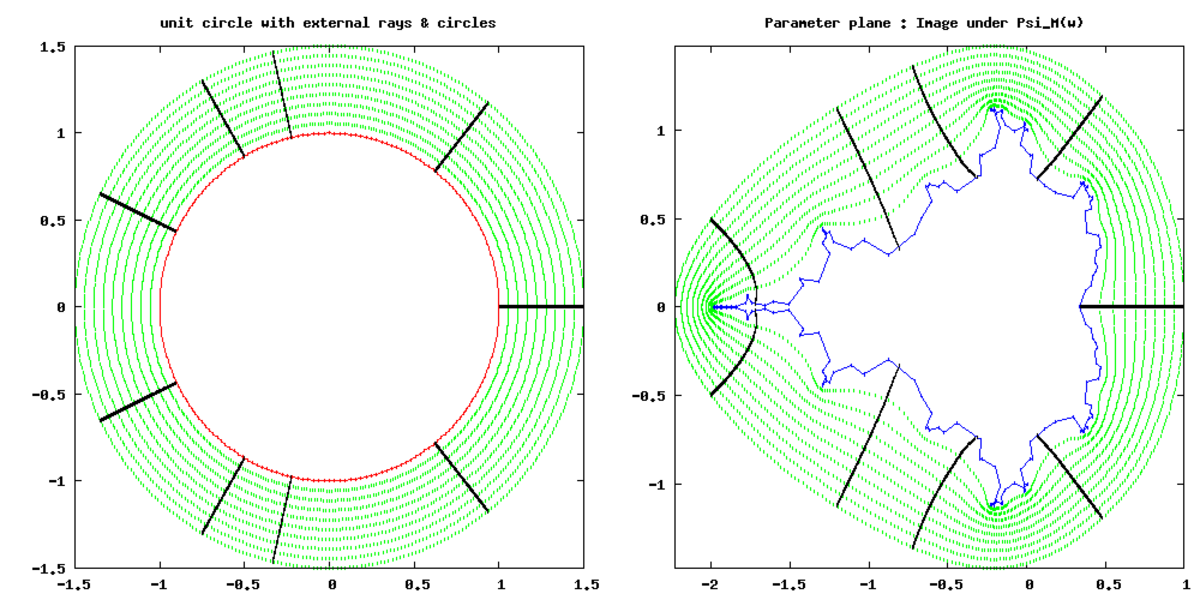
Dans ces cas, il est possible de construire explicitement les bijections holomorphes dont l'existence est affirmée par le théorème de Riemann : on trouvera plus de détails à l'article Dynamique holomorphe.