Théorème de Hahn-Banach - Définition
La liste des auteurs de cet article est disponible ici.
Quelques autres versions du théorème
On trouvera ci-dessous deux variantes de la « forme analytique » qui se déduisent facilement de celle mise en relief. La première fournit une variante du résultat pour les espaces vectoriels complexes ; la seconde précise que sous une bonne hypothèse de symétrie de p, notamment vérifiée quand p est une semi-norme, on peut obtenir une majoration de la valeur absolue (ou du module dans le cas complexe) de la forme linéaire prolongée.
Théorème — Soit V un espace vectoriel sur


Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
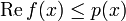
Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
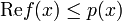
Théorème — Soit V un espace vectoriel sur



On suppose en outre que p possède la propriété de symétrie suivante : pour tout scalaire θ avec | θ | = 1 et tout vecteur x de V, p(x) = p(θx).
Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
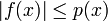
Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
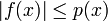
On trouvera des variantes de la forme géométrique à l'article Séparation des convexes.
Un exemple d'application en analyse fonctionnelle
Le corollaire suivant illustre comment le théorème de Hahn-Banach peut produire très facilement des résultats essentiels d'analyse fonctionnelle.
Corollaire — Soit E un espace normé, G un sous-espace de E et f une forme linéaire continue sur G. On peut alors prolonger f en une application continue définie sur E, de même norme que f.
On note
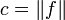
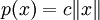
Il est inutilement long mais instructif de résoudre la question en utilisant la forme géométrique du théorème de Hahn-Banach : au lieu de penser à la fonction convexe p, on peut aussi penser au convexe ouvert C dont elle est la jauge, à savoir la boule ouverte de centre 0 et de rayon 1 / c. Si on veut se lancer dans cette voie, il faut introduire alors le sous-espace affine L, ensemble des points de G où f(x) = 1. On l'étend en un hyperplan fermé en appliquant Hahn-Banach ; la forme linéaire continue g pour lequel cet hyperplan est l'ensemble d'équation g(x) = 1 répond alors au cahier des charges.
Le rôle de l'axiome du choix
Comme on l'a vu, le lemme de Zorn (équivalent à l'axiome du choix) entraîne le théorème de Hahn-Banach. En réalité, le lemme des ultrafiltres, qui est une proposition plus faible que l'axiome du choix, est suffisant pour démontrer le théorème de Hahn-Banach. Mais inversement, on sait depuis des travaux de D. Pinas de 1972 que le théorème de Hahn-Banach n'est pas suffisant pour démontrer le lemme des ultrafiltres. Ainsi, le théorème de Hahn-Banach n'est pas équivalent à l'axiome du choix dans le système d'axiomes de Zermelo-Fraenkel. On doit ajouter à cela que le seul système de Zermelo-Fraenkel n'est pas à lui seul suffisant pour démontrer Hahn-Banach, dont toute preuve doit donc reposer inévitablement sur une ou autre variante de l'axiome du choix.

















































