Théorème fondamental de la géométrie projective - Définition

Introduction

Deux théorèmes de la géométrie projective s'appellent théorème fondamental de la géométrie projective :

• le premier théorème fondamental de la géométrie projective affirme que, quels que soient les repères projectifs d'un espace projectif de de dimension finie sur un corps commutatif, il existe une unique homographie qui envoie l'un sur l'autre;
• le second théorème fondamental de la géométrie projective affirme que toute bijection entre des espaces projectifs sur des corps de dimensions supérieurs à 2 qui envoie toute droite sur une droite est induite par une bijection semi-linéaire.

Premier théorème fondamental de la géométrie projective

Premier théorème fondamental de la géométrie projective

Soit K un corps (commutatif ou non) et E et F des espaces vectoriels de dimension finie n supérieur ou égale à 2 sur K. On appelle repère projectif de l'espace projectif P(E) déduit de E tout (n + 1)-uplet de points de P(E) tel qu'aucun de ces points n'appartient à sous-espace projectif de P(E) engendré par les n autres points (le plus petit sous-espace projectif qui contient ces points, pour l'inclusion).

Si n = 1, alors E est un plan vectoriel sur K et P(E) est une droite projective sur K. Les repères projectifs de P(E) ne sont autres que les triplets de points distincts de P(E) (c'est alors purement ensembliste).

Premier théorème fondamental de la géométrie projective. Soient (x_i) et (y_i) des repères projectifs de P(E) et P(F). Il existe une homographie f de P(E) sur P(F) (c'est-à-dire la bijection de P(E) sur P(F) déduite d'un isomorphisme d'espaces vectoriels de E sur F) telle que f(x_i) = y_i pour i = 1, ..., n + 1, et, pour qu'il en existe une seule, il faut et il suffit que K soit commutatif. Si E = F, cela signifie que le groupe projectif PGL(E) de E agit transitivement sur l'ensemble des repères projectifs de P(E), et pour qu'il y agisse simplement transitivement, il faut et il suffit que K soit commutatif.

On suppose que K est commutatif et que n = 2. Le théorème affirment donc que, quels que soient les points distincts x, y et z de P(E) et les points distincts s, t et u de P(F), il existe une unique homographie f de P(E) sur P(F) telle que f(x) = s, f(y) = t et f(z) = u. En particulier, si E = F, le groupe PGL(E) opère triplement transitivement sur P(E).

On suppose toujours que K est commutatif et que n = 2. Soient a, b, c et d des points de P(E) tels que a, b et c sont distincts. Il existe donc une unique homographie f de P(E) sur la droite projective P₁(K) = K ∪ {∝} telle que f(a) = ∝, f(b) = 0 et f(c) = 1, et alors f(d) est l'élément de K ∪ {∝} qu'est le birapport de (a, b, c, d). On a donc ici une définition géométrique du birapport.

Premier théorème fondamenal de la géométrie projective plane du point de vue synthétique

En géométrie projective du plan, le théorème fondamental est une base de démonstration puissante, qui permet pratiquement de tout démontrer. Mais il est un peu frustrant dans la mesure où il est trop puissant pour certaines petites propriétés, il ne permet pas de comprendre vraiment pourquoi telle petite propriété est vraie. C'est comme si l'on prenait, afin de rendre l'image concrète, un marteau-pilon pour écraser une mouche.

Tout dépend des axiomes que l'on a décidé d'utiliser. Dans ce cas précis, les axiomes sont :

les axiomes du plan projectif-tout-court:

• Un plan projectif est un ensemble
• C'est un ensemble de points
• Certains sous-ensembles s'appellent des droites.

les axiomes du plan projectif d'incidence:

• Il existe au moins 2 points dans le plan.
• Chaque droite possède au moins 3 points.
• Pour deux points distincts il existe une et une seule droite qui leur est incidente.
• Deux droites distinctes ont un et un seul point commun.
• Pour toute droite il existe au moins un point non incident à cette droite.

Plus l'axiome du plan projectif fondamental:

• Si une transformation projective unidimensionnelle possède 3 points fixes distincts, alors c'est la transformation identité.

Deux transfos projectives T1 et T2

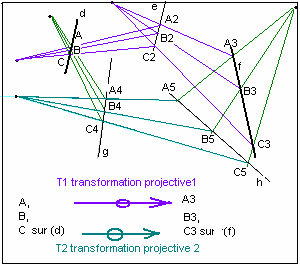
Le théorème fondamental de la géométrie projective plane s'énonce ainsi:

Il existe une et une seule transformation projective d'une division rectiligne en elle-même ou en une autre division rectiligne, transformant 3 points distincts de la première en trois points distincts de la seconde.

Le vocabulaire est étrange et s'explique par les tâtonnements dans la découverte des concepts de plus en plus nuancés.

• Configuration unidimensionnelle (en: one-dimensional-form): (2 cas) ensemble de points incidents à une même droite, appelé aussi division rectiligne, ou ensemble de droites incidentes à un même point, appelé aussi faisceau de droites (en: pencil of lines).
• Transformation projective, projectivité (en: projectivity): composition de perspectives.
• Perspective: (4 cas) soit une bijection entre une division rectiligne et un faisceau telle qu'un point et sa droite-image sont incidents (en: elementary correspondance); soit la bijection inverse; soit la combinaison des deux dans un ordre ou dans l'autre (en: perspectivity).
• Transformation projective unidimensionnelle: c'est une expression pléonastique pour rappeler que cette transformation projective ne travaille que sur des êtres unidimensionnels du plan ou de l'espace de dimension supérieure.
• Réf: Atlas des mathématiques, Fritz Reinhardt et Heinrich Soeder,1974, la Pochothèque en français 1997.
• réf pour l'anglais: Coxeter, 1987. Les anglais ont adopté le vocabulaire de Poncelet, les Français celui de Chasles.

On devrait en toute rigueur l'appeler le théorème fondamental de la géométrie plane projective mais l'usage en a décidé autrement.

Il faut démontrer l'existence et l'unicité.

Unicité. Admettons qu'il existe une éventuelle première transformation projective T1 qui transforme A, B, C en A3, B3, C3. En existe-t-il d'autres ? Soit une deuxième transformation projective T2 qui a la même propriété. Comme les transformations projectives sont bijectives, on peut considérer l'inverse de T2 (=T2⁻¹ ). Considérons maintenant la transfo composée P=T2⁻¹(T1()) Elle transforme A en A, B en B et C en C. Elle possède 3 points fixes distincts, alors d'après l'axiome ci-dessus c'est la transformation identité; P=I.

Or, par définition de T2⁻¹, I=T2⁻¹(T2()). Nous pouvons transformer cette équation:

T2⁻¹(T1()) = T2⁻¹(T2()). Combinons à gauche avec T2

T2[T2⁻¹(T1())] = T2[T2⁻¹(T2())]. Appliquons l'associativité de cette loi de composition interne

T2(T2⁻¹[T1()]) = T2(T2⁻¹[T2()]). Remplaçons T2(T2⁻¹ par I

I [T1()] = I [T2()] et, I étant l'élément neutre,

T1() = T2(), ce qui démontre l'unicité d'une éventuelle transformation projective T1 qui transforme A B C en A3, B3 C3.

Nota.Pour la notation de la loi de composition interne des transformations, on a le choix entre T2 o T1 qui se prononce "T2 rond T1" et signifie "on applique T1 puis T2" et l'autre notation par parenthésages-gigognes T2 (T1 ( ...etc = "T2 de T1 de...etc". Cette dernière notation est adoptée ici.

Existence.

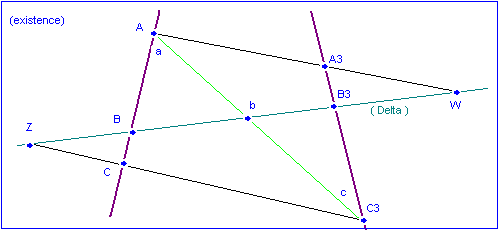
Existe-t-il au moins une transfo projective unidimensionnelle qui transforme ABC en A3B3C3?

Ici l'existence est explicitée uniquement pour le cas où 4 couples sont faits de points distincts, à savoir B3,B; C3,C; A3,A et C3,A. Soient Delta la droite B-B3, Z=Delta inter C-C3, W=Delta inter A-A3, b=Delta inter A-C3. D'abord précisons que ces droites et ces points existent toujours à cause des axiomes du plan projectif d'incidence rappelés supra. Les points auxiliaires a et c sont en fait confondus avec A et C3. On considère 2 transfo projectives unidimensionnelles:

Tz de centre Z qui transforme A, B, C en a, b, c.

Tw de centre W qui transforme a, b, c en A3, B3, C3.

formons la transformation composée U=Tw(Tz()).

U transforme A B C en A3 B3 C3. L'existence est donc démontrée.

Commentaire sur l'aspect axiomatique: cette démonstration de l'unicité peut paraître décevante dans la mesure où elle découle mécaniquement de l'axiome des 3 points fixes. Ce n'est que reculer pour mieux sauter, mais on n'y peut rien, c'est la démarche axiomatique. Si on veut remonter plus loin dans les axiomes, il faut par exemple démontrer le théorème suivant:"Si une transformation projective unidimensionnelle possède 3 points fixes distincts, alors c'est la transformation identité." Pour ce faire, on doit partir d'un système d'axiomes plus amont.

Une référence: (en:) Projective Geometry, H.S.M. Coxeter, Springer, 1987, 1998. Chap 2.1.Axioms