Théorie de jauge - Définition

Introduction

En physique théorique, une théorie de jauge est une théorie des champs basée sur un groupe de symétrie locale, appelé groupe de jauge, définissant une « invariance de jauge ». Le prototype le plus simple de théorie de jauge est l'électrodynamique classique de Maxwell.

L'expression « invariance de jauge » a été introduite en 1918 par le mathématicien Hermann Weyl.

Description mathématique

On considère un espace-temps classique modélisé par une variété différentielle lorentzienne à quatre dimensions, pas nécessairement courbe.

Champs de jauge et espaces fibrés

Les théories de champs de jauge dans l'espace-temps utilisent la notion d'espace fibré différentiel. Il s'agit encore d'une variété différentielle, mais de dimension plus grande que celle de l'espace-temps, qui joue ici le rôle d'espace de base du fibré.

On considère plus précisément un fibré principal, dont la fibre s'identifie au groupe de structure qui est un groupe de Lie précisant la symétrie de la théorie, appelée « invariance de jauge ».

Un champ de jauge A y apparait comme une connexion, et la forme de Yang-Mills associée F = dA comme la courbure associée à cette connexion.

Quelques groupes de Lie

Principaux groupes de Lie

• O(n) est le groupe orthogonal sur d'ordre n, i.e. le groupe multiplicatif des matrices n × n réelles orthogonales (vérifiant ^tMM = I_n).
• SO(n) est le groupe spécial orthogonal sur d'ordre n, i.e. le groupe multiplicatif des matrices n × n réelles orthogonales et de déterminant égal à 1 (^tMM = I_n et det M = 1).
• U(n) est le groupe unitaire sur d'ordre n, i.e. le groupe multiplicatif des matrices n × n complexes unitaires (vérifiant M*M = I_n).
• SU(n) est le groupe spécial unitaire sur d'ordre n, i.e. le groupe multiplicatif des matrices n × n complexes unitaires et de déterminant égal à 1 (M*M = I_n et det M = 1).

Cas particuliers

• O(1) = {1, -1}
• SO(1) = {1}.
• U(1) = SU(1) est le cercle unité complexe. Il est égal à
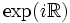
• SO(2) est isomorphe à U(1) : c'est l'ensemble des rotations du plan laissant 0 invariant.
• SO(3) est l'ensemble des rotations de l'espace à 3 dimensions.

Exemples physiques

Ont été démontrées pertinentes pour le monde réel :

• la théorie de jauge classique U(1), qui s'identifie à la théorie électromagnétique de Maxwell. C'est une théorie abélienne, qui admet des extensions non-abéliennes intéressantes appelées théories de Yang-Mills, basées sur les groupes non-abéliens SU(n).

• Après quantification, deux des théories de Yang-Mills constituent l'actuel « modèle standard » de la physique des particules :
  • le modèle électro-faible de Glashow, Salam et Weinberg est basé sur le groupe U(1) x SU(2) et décrit de façon unifiée l'électromagnétisme et l'interaction nucléaire faible.
  • la chromodynamique quantique est basée sur le groupe SU(3), et décrit l'interaction nucléaire forte entre les quarks et les gluons.