Univers d'Einstein - Définition

Introduction

L'univers d'Einstein est le nom qui a été donné au premier modèle cosmologique basé sur la théorie de la relativité générale découverte par Albert Einstein en 1915. Le modèle a été proposé par Einstein lui-même en 1917, mais a été abandonné suite à la découverte de l'expansion de l'univers.

Description

L'univers d'Einstein est basé sur le principe cosmologique proposé par Einstein pour l'occasion, à savoir l'idée que l'univers est homogène et isotrope. Pour des raisons qui semblent d'ordre philosophique, Einstein lui a adjoint l'hypothèse que celui-ci était statique, immuable. Sous l'effet de la gravité, les différents objets de l'univers s'attirent les uns les autres et ont donc tendance à se rapprocher. Pour contrebalancer cette attraction, Einstein a été amené à introduire l'équivalent d'une force répulsive dans l'univers, qu'il a appelé constante cosmologique. Cette hypothèse, qui rétrospectivement apparaît extrêmement ad hoc au vu du contexte, permet d'établir un équilibre entre phénomènes attractifs et répulsifs. Pour que cet équilibre puisse exister, il est nécessaire que la courbure spatiale de l'univers soit positive, autrement dit que l'univers soit d'extension finie, mais sans bord, un peu comme la sphère bidimensionnelle ordinaire. La staticité de l'univers est alors assurée si une certaine relation entre constante cosmologique, densité de matière et courbure spatiale est satisfaite.

Description mathématique

Dérivation de la solution

L'univers d'Einstein étant homogène et isotrope, il peut être décrit dans le cadre du formalisme de Friedmann-Lemaître-Robertson-Walker et des équations de Friedmann. Celles-ci s'écrivent

,

,

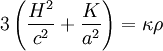
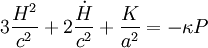
où P et ρ sont respectivement la pression et la densité d'énergie totales, H le taux d'expansion, K / a² la courbure spatiale, c la vitesse de la lumière et κ la constante d'Einstein. L'univers d'Einstein étant statique, son taux d'expansion est nul, et sa dérivée temporelle l'est également. On a ainsi

,

.

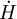
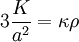
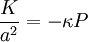
Le cas où la densité d'énergie et la pression sont nulles correspond à l'espace de Minkowski habituel. On voit que ces deux égalités ne peuvent par contre pas simultanément être satisfaites pour de la matière non relativiste, dont la pression est négligeable devant la densité d'énergie. De plus, si la densité d'énergie est non nulle, alors la pression totale doit être de signe opposé à la densité d'énergie (et égale au tiers de cette dernière en valeur absolue). Si l'on suppose que de la matière ordinaire est présente dans l'univers, le seul moyen de rendre compatible ces équations est de supposer l'existence d'une autre forme de matière aux propriétés exotiques. Plusieurs choix existent; celui d'Einstein correspondant à une constante cosmologique, qui peut s'interpréter comme un fluide dont la pression P_Λ est opposée à la densité ρ_Λ. En notant ρ_m la densité d'énergie sous forme de matière non relativiste, il vient alors

,

.

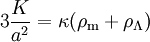
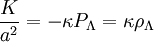
On obtient ainsi immédiatement

,

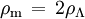
et la courbure spatiale est alors donnée par

.

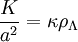
La raison de ce choix particulier d'une constante cosmologique de la part d'Einstein résulte du fait que la constante cosmologique peut, selon les cas, être considérée comme un fluide possédant une certaine densité d'énergie et une pression, soit comme une caractéristique purement géométrique de l'espace. Dans ce second cas, la constante cosmologique Λ représente une quantité homogène au carré d'une longueur, donnée par

.

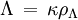
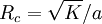
Dans ce cas, le rayon de courbure se déduit de la constante cosmologique par la formule

.