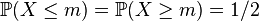Variable aléatoire réelle - Définition
La liste des auteurs de cet article est disponible ici.
Quelques variables aléatoires réelles
En guise d'introduction aux définitions concernant les variables aléatoires réelles, il semble intéressant de présenter brièvement une famille de variables très utilisées.
Outre la variable certaine qui prend une valeur donnée avec une probabilité égale à 1, la variable aléatoire réelle la plus simple est appelée variable de Bernoulli. Celle-ci peut prendre deux états, qu'il est toujours possible de coder 1 et 0, avec les probabilités p et 1-p. Une interprétation simple concerne un jeu de dé dans lequel on gagnerait un euro en tirant le six (p = 1/6). Sur une séquence de parties, la moyenne des gains tend vers p lorsque le nombre de parties tend vers l'infini.
Si on considère qu'une partie est constituée par n tirages au lieu d'un seul, le total des gains est une réalisation d'une variable binomiale qui peut prendre toutes les valeurs entières de 0 à n. Cette variable a pour moyenne le produit np. On obtient un exemple moins futile en considérant le score d'un candidat dans un sondage électoral.
Si n est assez grand et p pas trop petit, on peut trouver une approximation convenable en utilisant la variable de Gauss. Dans les sondages cela permet d'associer un intervalle de confiance au résultat brut. Ainsi, il y a 95 chances sur 100 pour qu'une enquête portant sur 1 000 personnes donne un résultat correct à ± 3 % près.
Toujours avec n grand, l'approximation de Poisson est préférable si p est assez petit pour que la moyenne np ne soit pas trop grande, de l'ordre de quelques unités. Dans un sondage ce serait la loi applicable aux « petits » candidats. C'est surtout la loi utilisée dans des problèmes de files d'attente.
La somme des carrés de ν variables de Gauss indépendantes est une variable de χ2 à ν degrés de liberté (la variable exponentielle en est un cas particulier). Le test du χ2 est utilisé pour apprécier la valeur de l'adéquation d'une loi de probabilité sur une distribution empirique.
Si on divise une variable de Gauss par une variable de χ (racine carrée de la précédente), on obtient une variable de Student. Le rapport de deux variables de χ2 indépendantes définit une variable de Snedecor. Ces deux lois sont utilisées dans l'analyse de populations supposées gaussiennes.
Simulation d'une variable aléatoire
On utilise souvent des générateurs pseudo aléatoires pour simuler le hasard. Il existe également des moyens d'exploiter l'indétermination de phénomènes physiques, par exemple en analysant les variations d'un film de lampe à lave, en analysant le bruit thermique, ou mieux encore, en demandant à la nature quantique de jeter des dés pour nous.
Outils pratiques
Moments et moments centrés
Le moment d'ordre un, espérance ou moyenne de la variable,
![\mu \equiv m_1= \mathbb{E}[X], \,](https://static.techno-science.net/illustration/Definitions/autres/f/fb1fbe6d11066aaada72be36a3ba42c3_a8842dfacd3edbd27d712f922a3ef22b.png)
est un indicateur de tendance centrale,
Les moments d'ordre supérieur éliminent ce paramètre de position en considérant la variable centrée par soustraction de sa moyenne.
Le moment centré d'ordre deux,
![\sigma^2\equiv m'_2 = \mathbb{E} \left [\left(X-\mu\right)^2\right], \,](https://static.techno-science.net/illustration/Definitions/autres/b/b20cedcd6803631d85db864586f93347_622679205d3ab0924729bbc68f434067.png)
est un indicateur de dispersion appelé variance. Sa racine carrée σ, grandeur homogène à la grandeur de base, s'appelle écart type. Lorsque la variable aléatoire est une valeur à un instant donné d'un processus aléatoire, l'expression moyenne quadratique est généralement préférée.
Ces deux moments fournissent une partie importante de l'information sur la variable, la totalité si celle-ci peut être considérée comme normale.
Les moments d'ordre supérieur, qui apportent pour les autres variables des précisions supplémentaires sur la forme de la distribution, portent sur la variable centrée réduite, rendue adimensionnelle par division par son écart type.
Le moment d'ordre trois de la variable centrée réduite,
![m'_3 =\mathbb{E} \left[ \left(\frac{X-\mu}{\sigma} \right)^3 \right], \,](https://static.techno-science.net/illustration/Definitions/autres/7/74f024a4bb7d0c2dfc3c79f9ba9c6b7c_86ec8e040dcd2c7234e8ce835f734204.png)
est un indicateur d'asymétrie.
Le moment d'ordre quatre de la variable centrée réduite,
![m'_4 =\mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right], \,](https://static.techno-science.net/illustration/Definitions/autres/c/ca024f3e1c739b245dc221f703c15d4f_676056ade152b4b9d5621eebc2968d10.png)
est un indicateur d'aplatissement des extrêmes des distributions appelé kurtosis.
Médiane et quantiles
On appelle médiane d'une variable aléatoire X, un réel m tel que
Dans le cas d'une variable aléatoire discrète, cette définition est peu intéressante car elle permet l'existence de plusieurs médianes
- si X est le numéro apparaissant sur la face supérieure d'un dé à 6 faces parfaitement équilibré, pour tout réel m strictement compris entre 3 et 4, on a :
-
ou bien l'existence d'une médiane qui ne donne pas une probabilité de 0,5
- Si X est la somme obtenue en lançant deux dés à 6 faces parfaitement équilibrés. X ne possède qu'une seule médiane 7 mais
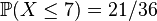
Dans le cas d'une variable continue, si la fonction de répartition est strictement croissante, la définition est équivalente à la suivante :
- la médiane de X est le réel unique m tel que
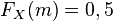
Le fait que la fonction de répartition soit continue, et supposée strictement croissante, à valeurs dans ]0 ; 1[, assure l'existence et l'unicité de la médiane.
Si la médiane a comme valeur m=0.5, il est possible cependant de s'intéresser à d'autres valeurs de m (que l'on nomme les quantiles) :