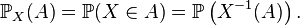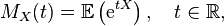Variable aléatoire réelle - Définition
La liste des auteurs de cet article est disponible ici.
Notions de base
Loi de probabilité
- La loi d'une variable aléatoire réelle décrit en détail la répartition des valeurs de cette variable. La loi de la variable X contient toutes les informations nécessaires pour calculer sa fonction de répartition, son espérance et plus généralement ses moments, sa fonction caractéristique, sa médiane et ses quantiles.
- En d'autres termes, si deux variables aléatoires réelles X et Y ont même loi de probabilité, alors elles ont même fonction de répartition, même espérance et plus généralement mêmes moments, même fonction caractéristique, même médiane et mêmes quantiles.
- La loi de probabilité d'une variable aléatoire réelle X est la donnée des valeurs
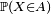
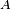
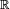
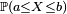
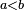
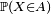
![\scriptstyle\ A=[a,b]](https://static.techno-science.net/illustration/Definitions/autres/c/c69cdfd1ca23902d4224d50bc3c11466_2b31385a1561cbeae6295340301da263.png)
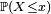
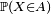
![\scriptstyle\ A=]-\infty,x]](https://static.techno-science.net/illustration/Definitions/autres/0/0960360dd3d96eecc4ed7a9e5d1dbdb9_f39e900f2fcd4a36e5e07b756f98717b.png)
- Selon sa définition mathématique (voir l'article variable aléatoire pour plus de détail), la loi de X est la mesure de probabilité
![\scriptstyle\ A=[a,b]](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c69cdfd1ca23902d4224d50bc3c11466_2b31385a1561cbeae6295340301da263.png)
![\scriptstyle\ A=]-\infty,x]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0960360dd3d96eecc4ed7a9e5d1dbdb9_f39e900f2fcd4a36e5e07b756f98717b.png)
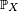
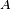
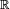
- La loi d'une variable aléatoire réelle peut être discrète ou posséder une densité (par rapport à la mesure de Lebesgue sur
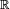
Fonction de répartition
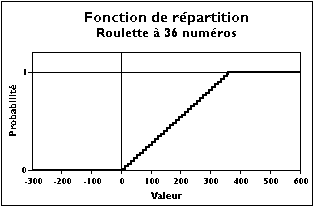
Il serait possible d'introduire cette notion à partir de l'une quelconque des variables précédemment considérées mais il paraît plus clair d'étudier le cas du dé sous un angle différent. En effet, il définit une variable aléatoire X qui prend avec la même probabilité d'apparition (1/6) des valeurs dans l'ensemble {1,2,3,4,5,6}. On peut alors associer à toute valeur réelle x la probabilité d'obtenir un tirage inférieur ou égal à x, ce qui définit une courbe en escalier dont les marches ont une hauteur égale à 1/6.
Formellement, cela conduit à une fonction de répartition
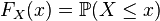
Dans celle-ci, la majuscule X représente la variable aléatoire réelle, ensemble de valeurs numériques, et la minuscule x représente la variable d'état, variable au sens usuel du terme.
Si les événements ne sont plus équiprobables, cela ne fait que déformer la courbe. Pour introduire une notion nouvelle, on peut commencer par remplacer le dé par une roulette à six numéros (ce qui conduit à un problème rigoureusement identique). Ensuite, on ne change rien de fondamental si on remplace les six nombres entiers par les repères des centres d'arcs de 60 degrés. À partir de là il est possible d'augmenter le nombre de secteurs en réduisant leur taille : les échelons deviendront de plus en plus petits jusqu'à être indiscernables sur un dessin. Le passage à la limite remplace la variable discrète par une variable continue qui prend toutes les valeurs réelles dans l'intervalle ]0,360] : c'est une variable uniforme.
Une fonction de répartition est croissante (au sens large) sur l'intervalle ]-∞,+∞[, et continue à droite en tout point ; elle tend vers 0 en -∞ et vers 1 en +∞. Réciproquement, toute fonction vérifiant les propriétés (caractéristiques) précédentes peut être considérée comme la fonction de répartition d'une variable aléatoire.
L'intérêt de la fonction de répartition réside dans le fait qu'elle est bien définie aussi bien pour les variables continues définies sur un ensemble continu que pour les variables discrètes définies sur un ensemble dénombrable (dans la plupart des cas pratiques il se réduit à un ensemble de valeurs équidistantes que l'on peut ramener à un ensemble d'entiers). Le remplacement progressif (l'approximation) d'une fonction de répartition dont la courbe est en escalier par une fonction de répartition dont la courbe est continue permet de voir intuitivement comment une variable continue peut fournir une approximation souvent plus facile à manipuler que la variable discrète originale. Voir l'article Convergence en loi pour une formulation plus mathématique de ce type d'approximation de variables discrètes par des variables continues.
Densité de probabilité d'une variable continue
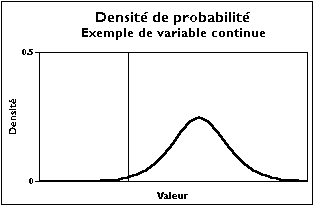
Une variable continue possède souvent une fonction de répartition continue en tout point et dérivable par morceaux. Il est alors commode de la dériver pour obtenir la densité de probabilité, vérifiant :
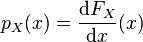
qui est définie et à valeurs positives (ou nulles) sur
![]-\infty,\, +\infty[\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d278f0180705c10ffa73acbea25f0949_6252211f3071d6a6994aa2b877050774.png)
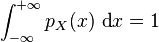
On reconstruit la fonction de répartition par la relation :
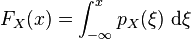
Dans les raisonnements généraux, il est souvent commode d'écrire ces formules sous forme différentielle :
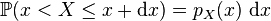
Si l'on effectue un changement de variable selon la formule
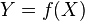
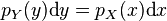
Fonction de probabilité et densité de probabilité d'une variable discrète
La loi d'une variable discrète est déterminée par l'ensemble des probabilités de ses valeurs nommé fonction de probabilité (mass function en anglais). Si l'on suppose qu'elle prend des valeurs entières (de signe quelconque), cela s'écrit :
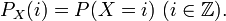
On reconstruit la fonction de répartition (dont les valeurs sont alors appelées probabilités cumulées) par la relation :
si
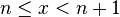
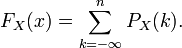
En considérant la fonction de répartition comme une somme d'échelons ou fonctions de Heaviside, sa dérivée peut s'interpréter comme une somme d'impulsions ou fonctions de Dirac. En posant
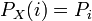
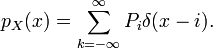
Cette « densité de probabilité » présente un intérêt dans un problème particulier. Lorsqu'une intégrale porte sur une densité de probabilité, la propriété fondamentale de la fonction de Dirac permet de transformer l'intégrale en une simple somme impliquant la fonction de probabilité.
Espérance mathématique
Définitions
L'espérance mathématique d'une variable aléatoire réelle se définit comme la valeur de cette variable pondérée par sa probabilité. Pour une variable continue, la formule différentielle donnée précédemment s'intègre, sous réserve d'intégrabilité, en
![\mathbb{E}[X] = \int_{-\infty}^{+\infty} x\ p_X(x)\ \textrm{d}x.](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a25705eebf6103e52601ed07a793e5f5_564c44e664bb4ed86411388b5cdb28d9.png)
Cette quantité est plus connue sous le nom de moyenne.
X étant une variable aléatoire réelle, une fonction f supposée régulière définit une nouvelle variable aléatoire
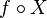
![\mathbb{E}[f(X)] = \int_{-\infty}^{+\infty} f(x)\ p_X(x)\ \textrm{d}x.](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/ee89bc246b13fceb34553cb7ca62867b_33a7b097b85c782ed419ecad6d02694d.png)
Pour une variable discrète, la « densité de probabilité » conduit, sous réserve de sommabilité, à
![\mathbb{E}[f(X)] = \sum_{k=-\infty}^{+\infty} f(k)\ P_X(k).](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a1b5506408f3280ba827b4a5898497b1_326f823577d05167a2b6c3da4136e5c9.png)
Fonction caractéristique
Si la densité de probabilité d'une variable aléatoire réelle X possède une transformée de Fourier, celle-ci (ou, plus précisément, la transformée inverse), fonction à valeurs complexes définie sur
![\phi_X(t) = \mathbb{E}[\textrm{e}^{itX}]\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2517b0eb24225415468de75f614e8da9_89010bc4542619fc7dbbd05c30ce8c44.png)
s'appelle fonction caractéristique de la variable.
Fonction génératrice des moments
La fonction génératrice des moments d'une variable aléatoire
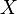
lorsque son espérance existe. Cette fonction, comme son nom l'indique, est utilisée afin de générer les moments associés à la distribution de probabilités de la variable aléatoire
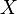
Moments
Si la fonction caractéristique (ou la fonction génératrice) d'une variable aléatoire est développable en série, celle- fait apparaître les moments de celle-ci, le moment d'ordre k étant défini comme
![m_k \equiv \mathbb{E}[X^k] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/72f81c526a3fb354ab241cc93dc07cf9_f3ba45e82a2d240726ed945755a607aa.png)
Dans le cas, important pratiquement, d'une variable assez régulière, celle-ci peut donc être caractérisée par la suite de ses moments, sa fonction caractéristique ou sa fonction génératrice, sa densité de probabilité ou, éventuellement, sa fonction de probabilité ou par sa fonction de répartition.
Dans le cas général, seuls les premiers moments peuvent exister.
