Polyèdre régulier - Définition
Un polyèdre est dit régulier s'il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques. Ils sont au nombre de neuf, dont cinq sont convexes et étaient connus de Platon. On appelle parfois polyèdres réguliers uniquement les solides de Platon.
Les solides de Platon

L'entourage de Platon les connaît en 400 av. J.-C. et Euclide les étudie dans ses Élements.
Il existe cinq solides de Platon :
Le tétraèdre régulier
- constitué de 4 faces en triangle équilatéral
- possède 4 sommets et 6 arêtes
Le cube
- constitué de 6 faces carrées
- possède 8 sommets et 12 arêtes
L'octaèdre régulier
- constitué de 8 faces en triangle équilatéral
- possède 6 sommets et 12 arêtes
Le dodécaèdre
- constitué de 12 faces pentagonales
- possède 20 sommets et 30 arêtes
L'icosaèdre
- constitué de 20 faces en triangle équilatéral
- possède 12 sommets et 30 arêtes
Les centres des faces d'un solide de Platon sont les sommets d'un solide de Platon. Cette correspondance est interne parmi les tétraèdres ; elle échange cubes et octaèdres d'une part, dodécaèdres et icosaèdres d'autre part.
.
Platon considérait ces solides comme l'image de la perfection ; pour lui, comme il l'explique dans son dialogue "Timée", le tétraèdre est le symbole du feu, l'octaèdre celui de l'air, l'icosaèdre celui de l'eau, le cube celui de la terre et le dodécaèdre celui de l'univers tout entier.
Les mathématiques modernes rattachent ces 5 solides réguliers à la notion de groupe.
Les polyèdres de Kepler-Poinsot
Outre les cinq solides de Platon, on peut construire quatre autres solides réguliers, deux dont les faces sont des polygones réguliers étoilés (ou croisés) : les solides de Kepler, et deux ayant des faces régulières, mais qui peuvent s'interpénétrer : les solides de Poinsot. 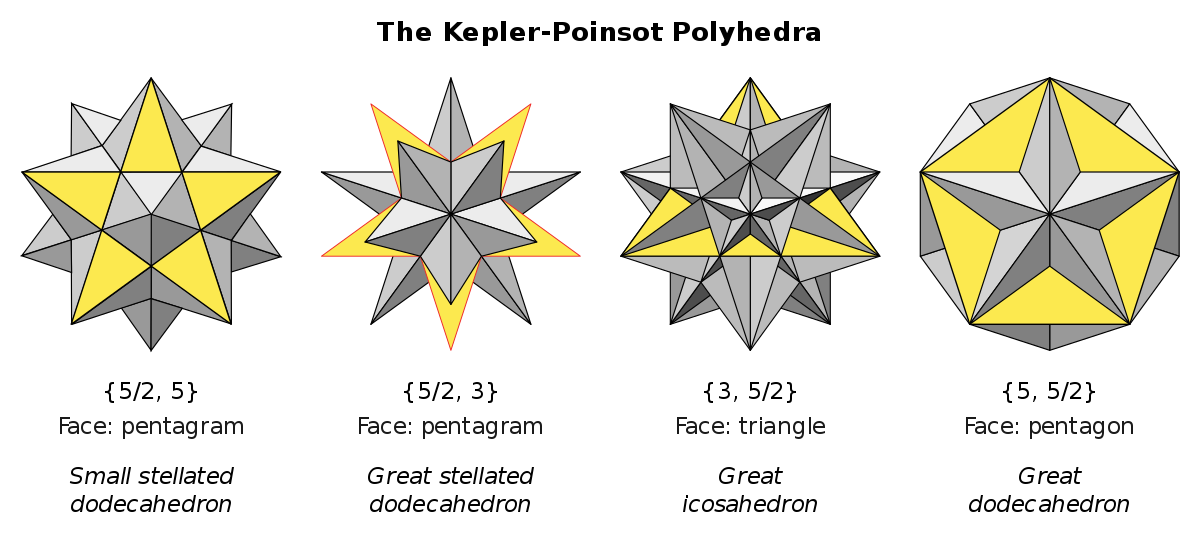
- Le petit dodécaèdre étoilé a été découvert par Kepler vingt-deux siècles après Platon, en 1619. Il a 12 faces qui sont des pentagones étoilés, 12 sommets et 30 arêtes. En chaque sommet se réunissent trois faces.
- Kepler a aussi découvert le grand dodécaèdre étoilé, formé des mêmes douze pentagones étoilés, qui a aussi 30 arêtes mais seulement 20 sommets.
- Poinsot découvre le grand dodécaèdre en 1809. Ses 12 faces sont des pentagones réguliers, il a 12 sommets et 30 arêtes.
- Il découvre enfin le grand icosaèdre, formé de 20 triangles équilatéraux, et qui possède 12 sommets et 30 arêtes.



