Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)
Une bulle de savon entortillée qui possède une poignée? Il est compréhensible que l'on trouve cela difficile à visualiser. Les experts pensaient même depuis plus de deux siècles qu'une telle structure était mathématiquement impossible. Mais plus maintenant.
Dans un rapport publié dans l'édition de novembre de Proceedings of the National Academy of Sciences, les mathématiciens Matthias Weber de l'Université de l'Indiana, David Hoffman de l'Université de Stanford et Michael Wolf de l'Université de Rice ont présenté la preuve de l'existence d'une nouvelle surface minimale dans une famille appelée "hélicoïde de genre un".
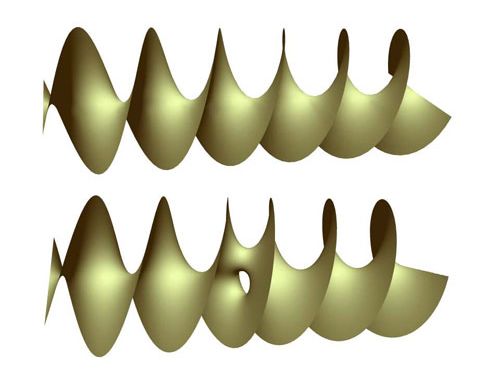
En haut: un hélicoïde traditionnel
En bas: le trou deviendrait une poignée si la forme était
totalement détordue en une surface plane
Un hélicoïde est la surface que l'on obtient quand une des formes les plus simples -une surface plane- est tordue un nombre infini de fois. Si l'hélicoïde est vertical, sa forme ressemble à la rampe d'accès à un parking à étage. La nouvelle surface ressemble à cet hélicoïde traditionnel à ceci près qu'elle possède une caractéristique supplémentaire: une poignée telle qu'on peut la trouver sur une tasse à café, ou, si l'on préfère, comme si une colonne supplémentaire était rajoutée au niveau d'un "étage" de la rampe de stationnement.
"Cette preuve nous indique que notre intuition n'était pas bien exacte au sujet ce qui est possible et ce qui n'est pas possible", remarque Weber. "Une raison probable à ce que l'on ne l'a pas découvert plus tôt est que personne n'avait imaginé que quelque chose de semblable pouvait exister".
Toutes les surfaces minimales ont quelque chose d'important en commun: une superficie minimale. "Une surface minimale se forme lorsque la pression des deux côtés d'une surface est identique", explique Weber. "Par exemple, quand on plonge un crochet recourbé dans de l'eau savonneuse, la bulle de savon qui se forme sur le crochet est une surface minimale". Ces bulles de savon peuvent avoir diverses formes, selon la forme du crochet, mais dans tous les cas la bulle essaye de réduire au minimum la tension superficielle et cela se produit quand la bulle a la plus petite superficie possible. En chacun de ses points, une surface minimale est soit plane, soit de la forme d'une selle de cheval (ou d'une pomme chips).
Des applications variées
Les surfaces minimales s'avèrent importantes au niveau moléculaire. "A l'échelle nanométrique, les surfaces de contact entre certaines substances sont des surfaces minimales", indique Weber. Par exemple, certains copolymères qui sont des plastiques employés pour fabriquer de nouveaux types de tissus. Le mélange de ces copolymères produit des surfaces minimales aux points de contact. Savoir à quoi ressemblent ces zones de contact peut aider à déterminer les futures propriétés chimiques du mélange."Les surfaces minimales sont extrêmement stables en tant qu'objets physiques, précise Weber, et cela peut être un avantage pour toute sorte de structure". Des architectes ont été intrigués par les illustrations numériques de certaines de ses surfaces minimales et étudient avec lui la possibilité de les adapter à des structures architecturales, intérieures ou extérieures.
Les qualités esthétiques des images numériques de Weber ne sont pas non plus sans intérêt: sa galerie montre des surfaces minimales placées dans des environnements imaginaires. "Ces images ne sont pas destinées à illustrer des concepts mathématiques", remarque Weber. "Elles atteindront leur but si les gens qui les regardent peuvent ressentir une partie de l'intrigant sortilège que ressent un mathématicien en explorant les objets mathématiques".
Dans une deuxième galerie, les images illustrent des concepts mathématiques. "C'est la plus complète collection de surfaces minimales accessible", indique Weber. "Les utilisateurs peuvent télécharger les programmes qui recréent les surfaces, leur permettant d'entreprendre des expériences numériques et visuelles".
La preuve complète des mathématiciens est longue de plus de 100 pages. Le résumé de leur rapport est disponible ici.
Populaires